二分搜索树(Binary Search Tree)
为什么要使用树?
比如说我们电脑有磁盘, 磁盘下面有很多文件夹, 每个文件夹都分门别类的存放自己要查找的东西。 假设有文学类文件夹、编程开发文件夹、画画文件夹等等等。
文学文件夹下又有散文、诗歌、小说、童话等等
编程文件夹下又有C++、JAVA、Python等等、
画画文件夹下又有油画、插画等等
每个大类下又分各种小类, 直到不能再细分到一个领域了。如果没有树结构的话, 我们如何能在大量文件中 查找到我们想要的书呢?即使能查到, 效率也是非常低的。
二叉树
在了解二分搜索树之前, 我们先来看看二叉树长什么样子。
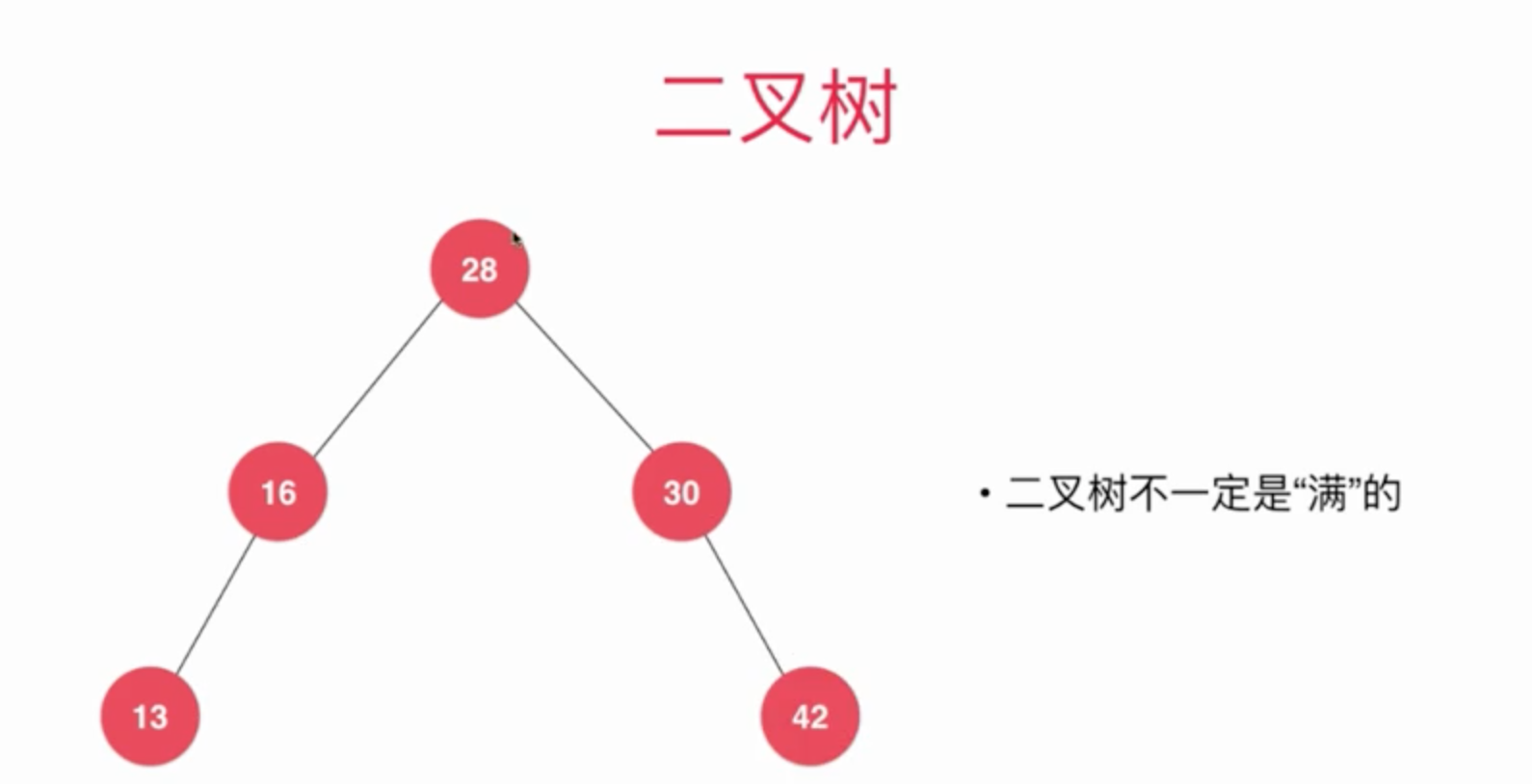
通过下图, 我们来大概了解一下什么是二叉树。
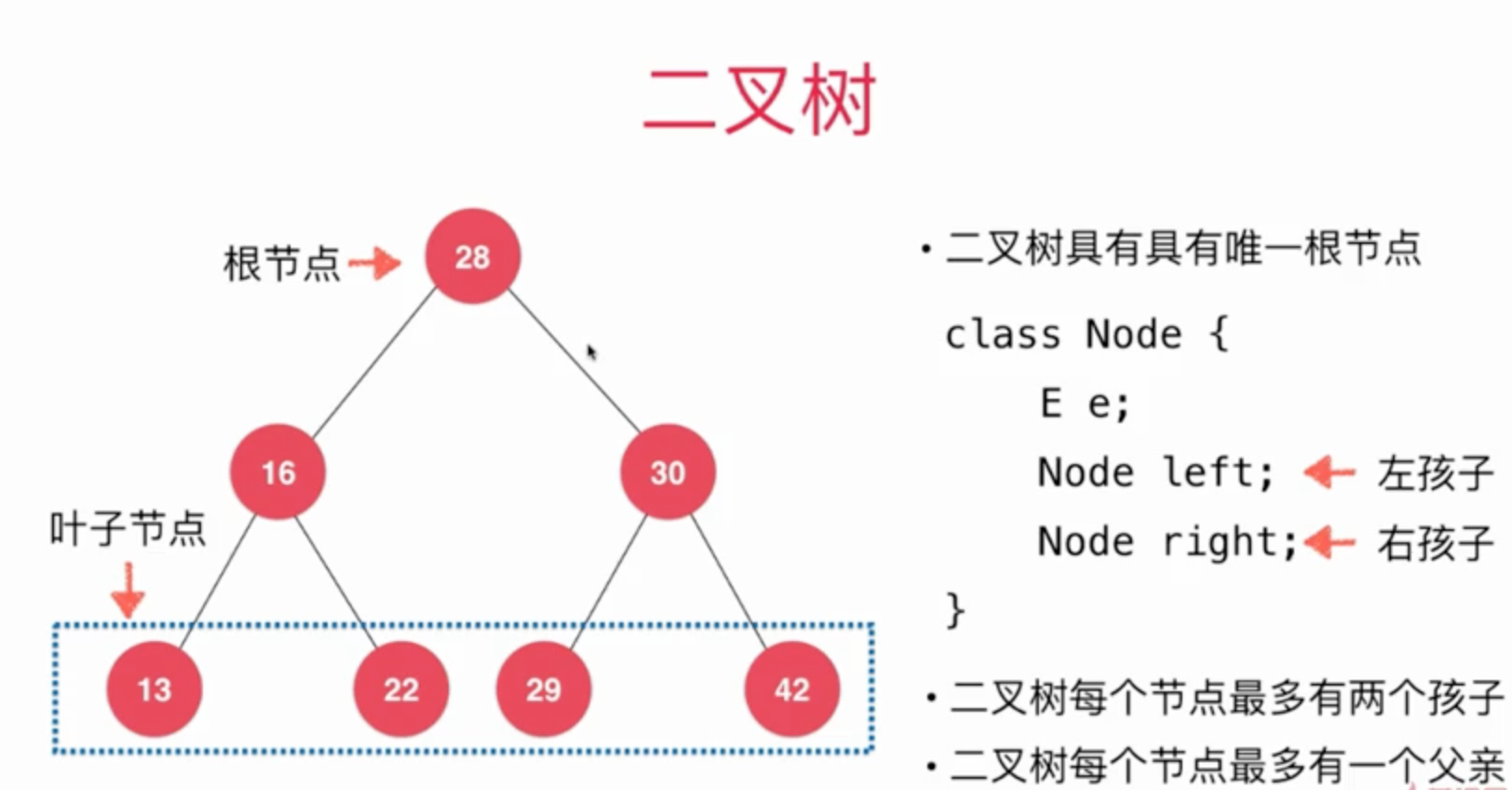
二叉树和链表一样属于动态数据结构。我们不需要在创建数据结构的时候, 就去决定这个数据结构能够存储多少元素的问题。 如果要添加元素, 就new一个新空间添加到数据结构中, 删除也是一样的。
更具上图, 我们如何构建一个二叉树?
class Node {
E e ;
Node left ; // 左孩子
Node right ; // 右孩子
}
二叉树居右唯一一个根节点就是28这个元素。
在创建节点的同时, 我们还可以指定我们左边和右边的孩子是谁, 比如上图中
元素28的左孩子是16右孩子是30
元素16的左孩子是13右孩子是22
元素30的左孩子是29右孩子是42
每个节点都有一个父亲节点, 除了根节点没有父节点外。
16的父亲节点是28
30的父亲节点是28
二叉树顾名思义就是, 每个节点最多只能分2个节点, 如果有多个节点我们可以更具它分为几个叉就称为几叉树(多叉树)。
如果一个孩子都没有的我们称为叶子节点(左右孩子都为空就是叶子节点)。
二叉树的递归
二叉树具有天然的递归性, 每个节点又可以看做是一个二叉树。
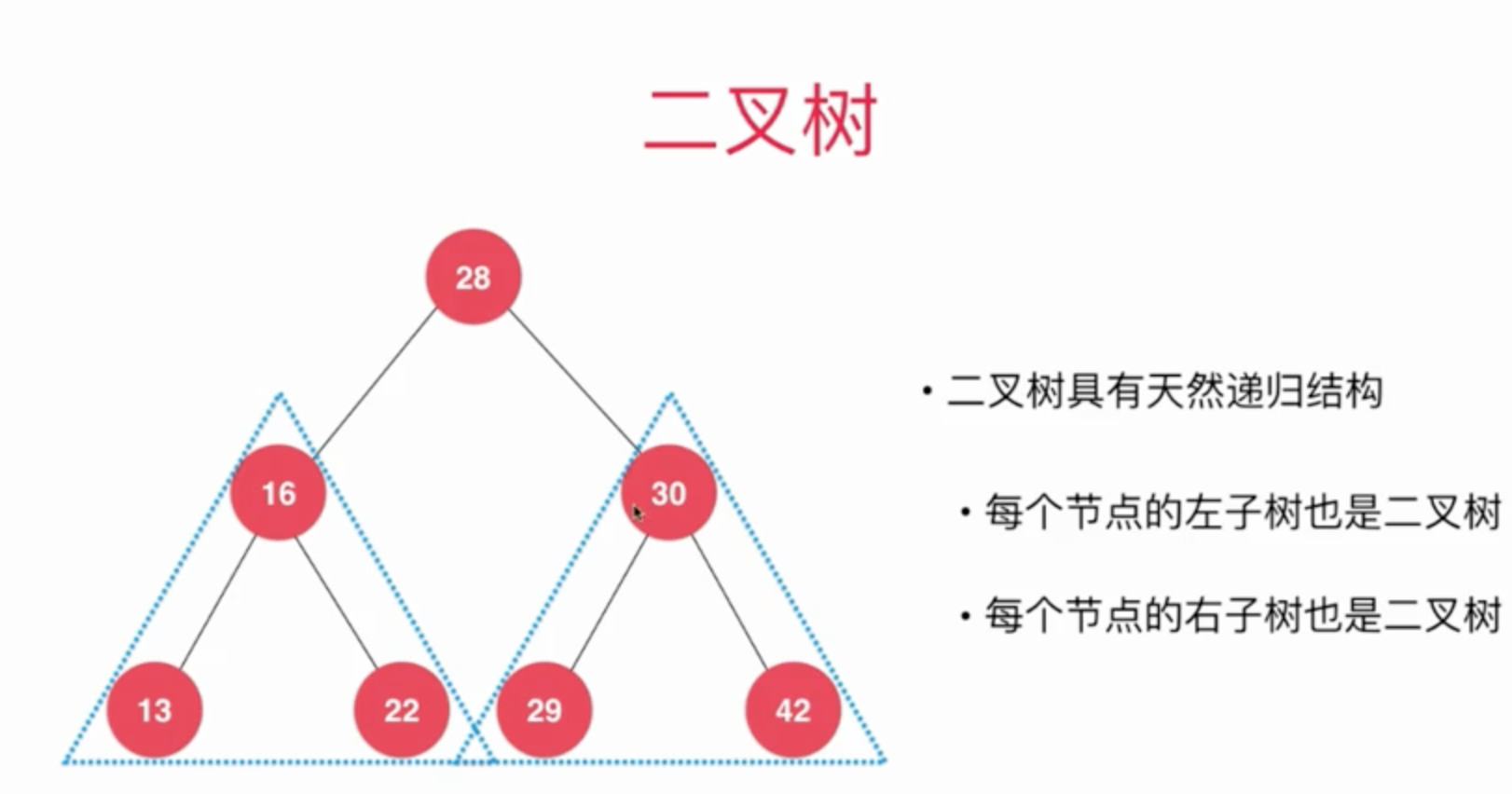
二叉树一些形态
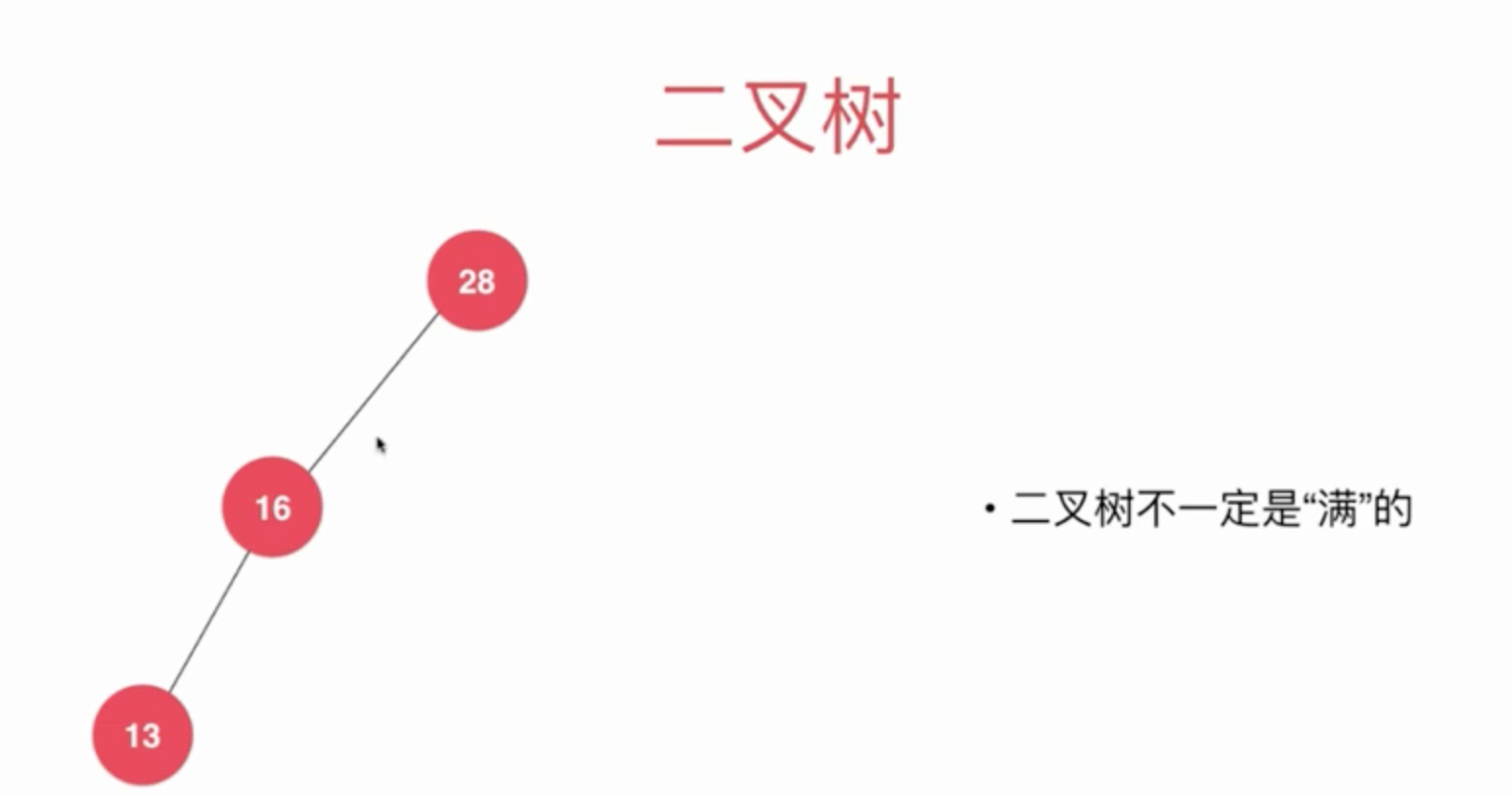
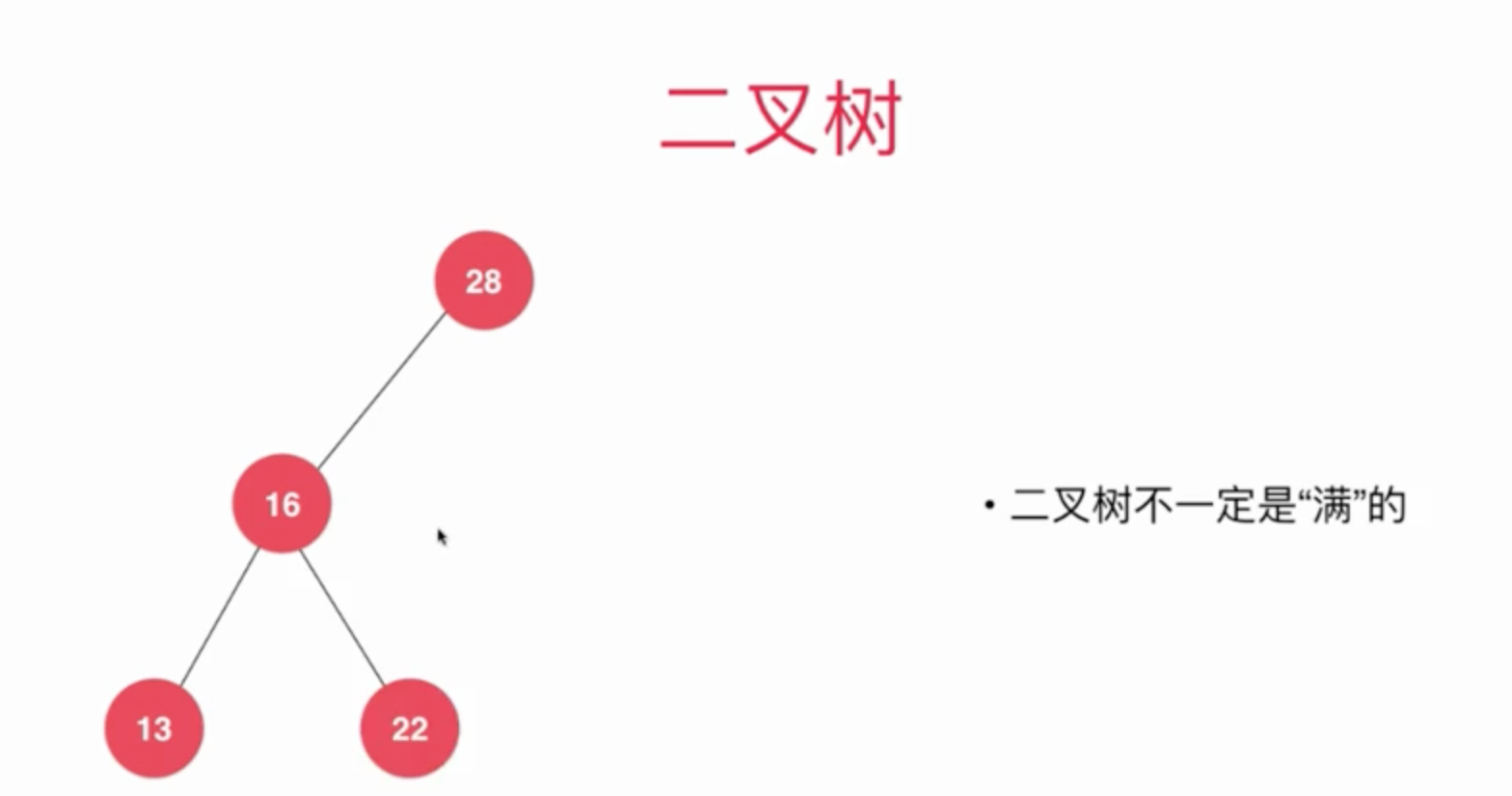
上面的话, 我们都是满二叉树, 但是很多时候都不是。如下图
只有一个节点或者为空的二叉树

只有左子树的二叉树
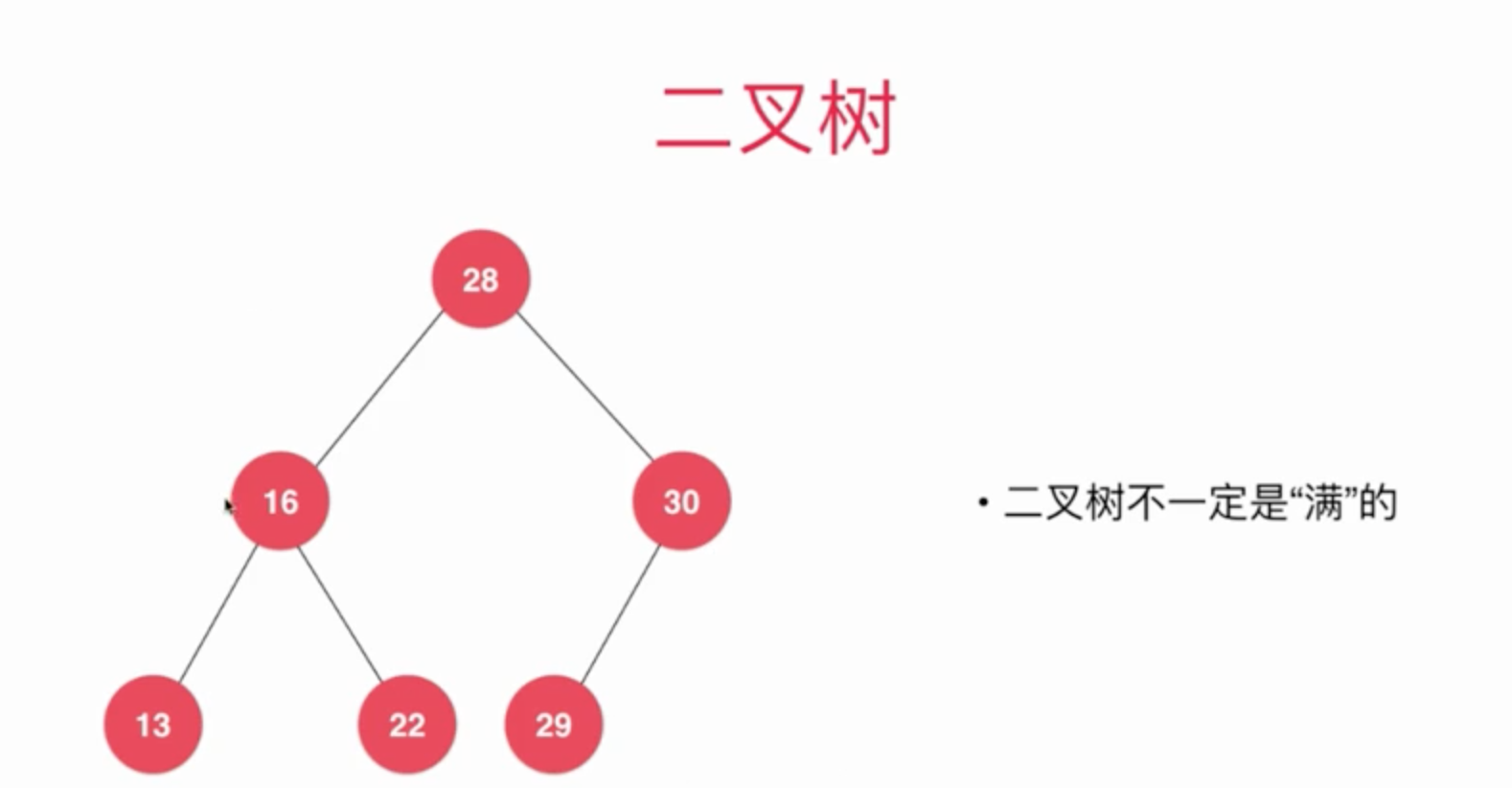
二分搜索树
定义:
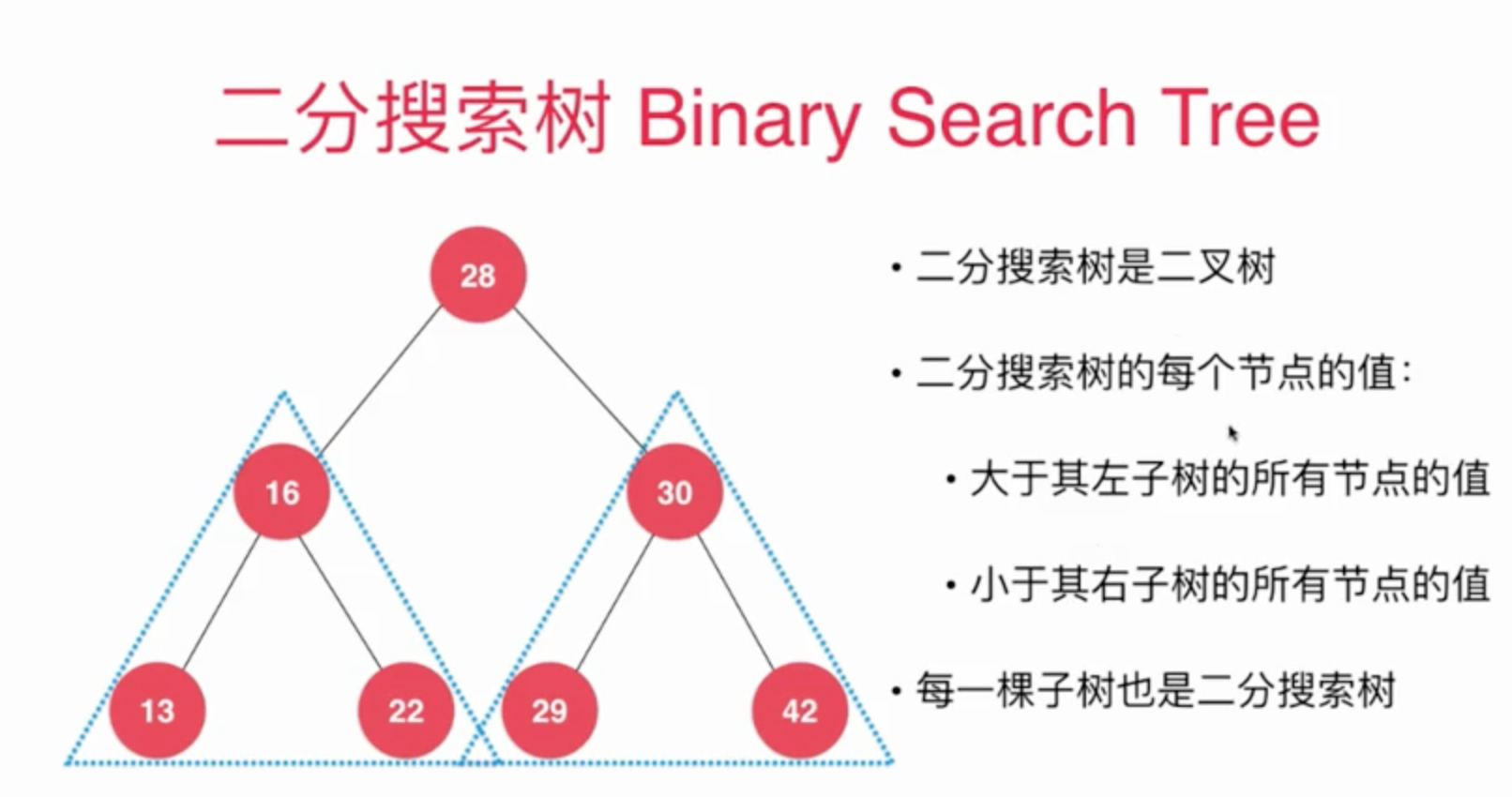
- 若任意节点的左子树不为空, 则左子树上所有及诶按的值均小于它的根节点值
- 若任意节点的右子树不为空, 则右子树上所有节点的值均大于它的更及诶按的值
- 任意节点的左、右子树分别为二分搜索树
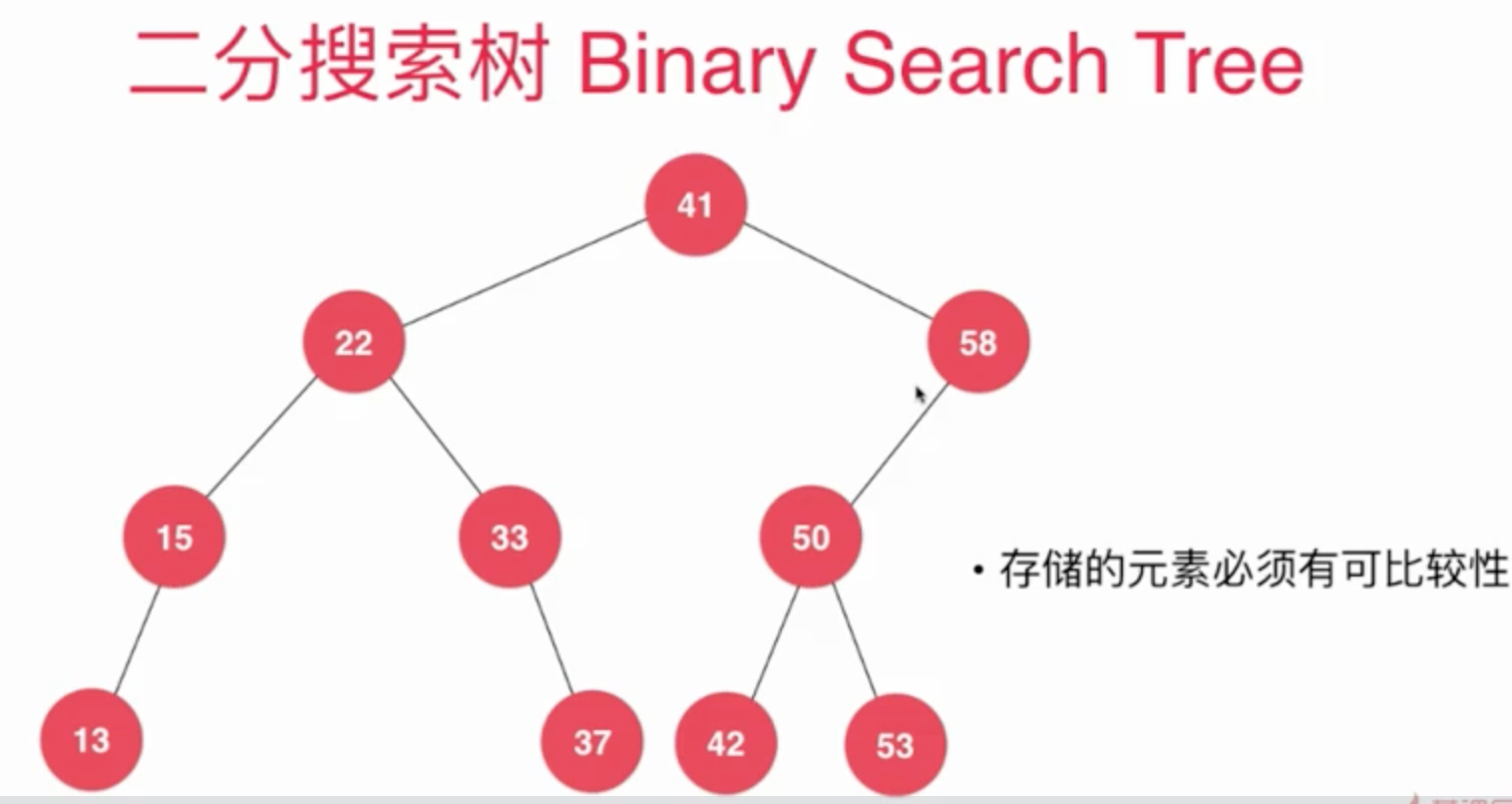
二叉树中每个元素都需要进行比较, 而且并不是都是一个满二叉树
实战部分
经过前面的学习, 我们已经大概清楚什么是二分搜索树了。下面我们通过代码来实现把。
/****
*
* 存储的元素需要有可比较性, 所以我们需要继承Comparable
* @param <E>
*/
public class BST<E extends Comparable<E>> {
private class Node {
E e ;
Node left ;
Node right ;
public Node(E e) {
this.e = e;
left = null ;
right = null ;
}
}
private Node root ;
private int size ;
public BST() {
this.root = null;
}
public int size() {
return size ;
}
public boolean isEmpty() {
return size == 0 ;
}
}
添加元素
如何向二分搜索树添加一个元素?
假设当前二分搜索树为NULL, 我们添加元素5就作为root
即: 5
/ \
如果现在在来一个元素3呢? 更具上面了解的特性, 应该放在树的左侧
即: 5
/ \
3 NULL
如果再来一个元素9那么则放在该树的右侧
即: 5
/ \
3 9
如果我们在加入一个元素9, 这里我们不进行插入, 我们的二分搜索树不会插入重复数据
现在, 我们有了一个简单的二分搜索树, 如果在插入新增的元素, 也是依次查询判断, 直到没有可以比较的节点, 就进行插入。
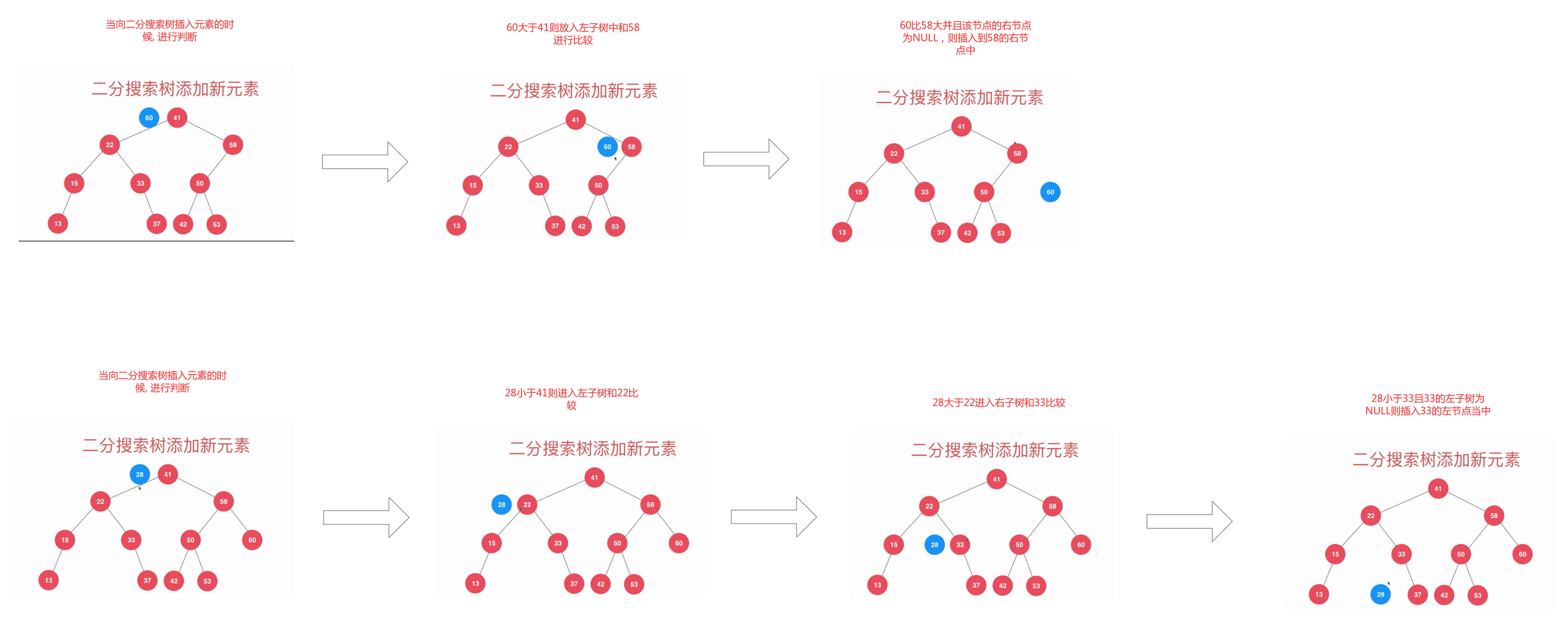
上面的图片也更加直观的展示如何插入一个元素了, 下面我们通过编写代码来实现如何插入元素。
public void add(E e) {
// 如果当前树节点为null, 直接让当前元素为root
if (root == null) {
this.root = new Node(e) ;
size ++ ;
} else {
// 如果树不为空, 则通过递归进行插入
add(root, e) ;
}
}
private void add(Node node, E e) {
if (e.compareTo(node.e) == 0) { // 如果是相同的值, 则直接终止
return ;
} else if (e.compareTo(node.e) < 0 && node.left == null) { // 如果小于并且该节点下面也没有元素了, 则插入该元素
node.left = new Node(e) ;
size ++ ;
return ;
} else if (e.compareTo(node.e) > 0 && node.right == null) { // 如果大于并且该节点下面也没有元素了, 则插入该元素
node.right = new Node(e) ;
size ++ ;
return ;
}
if (e.compareTo(node.e) < 0) {
add(node.left, e);
} else {
add(node.right, e);
}
}
上面的方法确实已经实现了我们插入元素的要求, 但是判断递归跳出条件却很繁琐。
假设遍历到node就是为空了, 表示已经没有节点可以判断, 我们只需要创建一个node并返回。
递归的特性返回到上一层并获取到返回值后, 我们只需要判断是>0还是<0来设置为挂接到左子树还是挂接到右子树中。
改进后的程序
public void add(E e) {
root = add(root, e);
}
private Node add(Node node, E e) {
// 当我们递归遍历到为空就表示当前节点已经到底了, 直接返回
if (node == null) {
size ++ ;
return new Node(e) ;
}
// 这里能将上一次返回的值获取到, 然后指定放在左子树还是右子树中
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
} else if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}
return node ;
}
图: 2
/ \
1 5
现在有这样的一棵二分搜索树, 然后我要添加元素9会是如何呢?
1. 判断当前节点是否为空
2. 判断当前元素插入左子树还是右子树中, 指向下一个节点
3. 直到节点为空, 否则一直执行步骤1和2
4. 当节点为空后, 创建新节点返回数据, 并设置该节点挂载到左子树或是右子树中。
即:
| | | | | nil |
| | | 5 | | 5 |
| 2 | | 2 | | 2 |
|-----| |-----| |-----|
当碰到null的时候返回新的值, 此时5我们已经判断他是大于的, 也就是5.right = 9
即: 2
/ \
1 5
\
9
以上就是如何向二分搜索树中插入一个元素全过程。
二分搜索树查找
如果上面的插入操作你已经理解了, 那么查找操作几乎是手到擒来。它比插入操作更简单, 因为不需要维护树的结构, 只需要判断是否存在。
public boolean contains(E e) {
return contains(root, e) ;
}
// 判断二分搜索树是否包含该元素
private boolean contains(Node node, E e) {
if (node == null) {
return false ; // 如果树为null, 则肯定不包含
}
if (e.compareTo(node.e) == 0) {
return true ; // 包含元素
} else if (e.compareTo(node.e) < 0) {
return contains(node.left, e) ;
} else {
return contains(node.right, e) ;
}
}
整体逻辑几乎是一模一样的, 所以这里不做过多的说明。
遍历
- 前序遍历
- 定义: 先访问根节点, 然后前序遍历左子树, 在前序遍历右子树(中, 左, 右)
前序遍历是怎么个遍历方式呢? 如下:
图: 5
/ \
3 6
/ \ \
2 4 8
更具上面的定义, 在设计一个递归函数的时候, 我们要先输出根节点, 然后递归左子树, 左子树没有节点后在遍历右子树。
输出: 5->3->2->4->6->8
public void preOrder() {
preOrder(root);
}
// 前序遍历二分搜索树
private void preOrder(Node node) {
if (node == null)
return ;
System.out.println(node.e);
preOrder(node.left); // 遍历左子树
preOrder(node.right); // 遍历右子树
}
现在我们重写toString方法, 利用前序遍历的方法来输出看看。
@Override
public String toString() {
StringBuffer res = new StringBuffer();
generateBSTString(root, 0, res);
return res.toString();
}
private void generateBSTString(Node node, int depth, StringBuffer res) {
if (node == null) {
res.append(generateDepthString(depth) + "null\n");
return ;
}
res.append(generateDepthString(depth) + node.e + "\n");
generateBSTString(node.left, depth + 1, res);
generateBSTString(node.right, depth + 1, res);
}
// depth深度, 这样加入--就能知道在不在一个层级
private String generateDepthString(int depth) {
StringBuffer res = new StringBuffer();
for (int i = 0; i < depth; i ++) {
res.append("--");
}
return res.toString();
}
上面的toString最终会输出如下结果集:
5
--3
----2
------null
------null
----4
------null
------null
--6
----null
----8
------null
------null
这样就知道3和6是同一个级别, 3是2的父节点
- 中序遍历
- 定义: 遍历根节点的左子树, 然后访问根节点, 最后遍历右子树(左中右)
图: 5
/ \
3 6
/ \ \
2 4 8
还是和上面一样的树结构, 如果不通过运行代码, 大家知道会输出什么结果吗?
输出: 2->3->4->5->6->8
你会发现输出来之后, 是一个有顺序的, 其实很正常所有左边的节点数据都比中间的值要小, 所有右边的数据都比中间值要大。所以输出来是一个有顺序的排列。
public void inOrder() {
inOrder(root);
}
// 中序遍历节点数据
private void inOrder(Node node) {
if (node == null) return ;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
- 后序遍历
- 定义: 从左到右先叶子后节点的方式遍历访问左右子树, 最后访问根节点(左右中)
图: 5
/ \
3 6
/ \ \
2 4 8
还是和上面一样的树结构, 如果不通过运行代码, 大家知道会输出什么结果吗?
输出: 2->4->3->8->6->5
public void postOrder() {
postOrder(root);
}
// 后序遍历
private void postOrder(Node node) {
if (node == null) return ;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
- 层次遍历
图: 5
/ \
3 6
/ \ \
2 4 8
输出: 5->3->6->2->4->8
层次遍历我们无法通过递归来实现, 我们需要借助队列来实现层次遍历。
第一次, 28进入队列, 然后获取28的左右子树(3和6)
第二次获取3的左右子树(2和4)
第三次获取6的左右子树(8)
F | 5 | F | 5 | F | 5 | F | 5 |
| | | 3 | | 3 | | 3 |
| | | 6 | | 6 | | 6 |
| | | | | 2 | | 2 |
| | | | | 4 | | 4 |
| | | | | | | 8 |
T | | T | | T | | T | |
通过上面直观的图例, 我们看看代码如何实现把.
// 层序遍历
public void levelOrder() {
Queue<Node> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
Node cur = q.remove();
System.out.println(cur.e);
if (cur.left != null)
q.add(cur.left);
if (cur.right != null)
q.add(cur.right);
}
}
删除
在进行任意元素删除, 我们先来做比较简单的操作, 删除最小和最大值开始。 已知二分搜索树的特性, 我们知道最左边的值就是最小值, 最右边的值就是最大值。
删除最小值流程:
第一次删除最小值13, 变成图2的值
图2中15成为最小的值, 就形成了图3的值, 如果我们在删除图3中最小值之后(由于节点22有右子树的值), 我们需要进行特殊处理。
在删除节点22最小值的时候, 我们只需要把22的右子树放置到41的左子树就可以了。最终结果就是图4了。
图1: 41 图2: 41 图3: 41 图4: 41
/ \ / \ / \ / \
22 58 22 58 22 58 33 58
/ \ / => / \ / => \ / => \ /
15 33 50 15 33 50 33 50 37 50
/ \ / \ \ / \ \ / \ / \
13 37 42 53 37 42 53 37 42 53 42 53
删除最大值流程:
第一次删除最大值63, 变成图2的值
当最大值为58的时候, 他有左子树的数据, 和删除最小值一样也需要特殊处理一下将58的左子树的值放到41的右子树上就可以了。
图1: 41 图2: 41 图3: 41
/ \ / \ / \
22 58 22 58 22 50
/ \ / \ => / \ / => / \ / \
15 33 50 63 15 33 50 15 33 42 53
/ \ / \ / \ / \ / \
13 37 42 53 13 37 42 53 13 37
我们通过代码先来查询出最小和最大值。
public E minimum() {
if (size == 0)
throw new IllegalArgumentException("BST is Empty");
return minimum(root).e;
}
// 查询二分搜索树最小值
// 其实这种完全就破坏树结构了, 和链表没区别了, 一直扫左边数据
private Node minimum(Node node) {
// 当前节点的left如果为空就表示当前节点为叶子节点退出递归条件
if (node.left == null)
return node ;
// 否则一直往左查询
return minimum(node.left);
}
public E maximum() {
if (size == 0)
throw new IllegalArgumentException("BST is Empty");
return maximum(root).e;
}
// 查询二分搜索树最大值
private Node maximum(Node node) {
// 当前节点的left如果为空就表示当前节点为叶子节点退出递归条件
if (node.right == null)
return node ;
// 否则一直往右查询
return maximum(node.right);
}
经过上面查找最小和最大值的基础, 其实我们在删除节点只不过是说要稍微处理一下左右子树的问题, 但其实和add()方法有点类似, 最后返回节点进行挂载.
public E removeMin() {
E e = minimum();
root = removeMin(root);
return e ;
}
// 删除掉以node为根的二分搜索树中最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
public E removeMax() {
E e = maximum();
root = removeMax(root);
return e ;
}
private Node removeMax(Node node) {
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
接下来就是最主要的操作了, 如何删除任意一个节点呢?
先来介绍删除任意节点的几种情况:
第一种情况: 删除只有左孩子的节点(简单)
如下图1, 如果我要删除的节点是58, 就和删除最大节点在逻辑是一样的, 把50节点挂载到41的右子树上。
需要注意点是: 只有左孩子的节点, 不一定是最大值所在的节点, 比如节点15这个节点他也是有左孩子的
图1: 41 图2: 41
/ \ / \
22 58 22 50
/ \ / => / \ / \
15 33 50 15 33 42 53
/ / \ /
13 42 53 13
第二种情况: 删除只有右孩子的节点(简单)
比如: 我们要删除节点为58的值, 它只有右孩子, 和删除最小值的逻辑基本一样。
所以在删除58的时候, 把58的右字数挂载到41的右子树上即可。
图1: 41 图2: 41
/ \ / \
22 58 22 60
/ \ \ => / \ / \
15 33 60 15 33 59 63
/ \ / \ / \
13 37 59 63 13 37
第三种情况: 删除左右都有孩子的节点(重点难点)
比如现在我们还是删除节点58的值, 但是左右孩子都不为空, 那如何处理呢?
1. 删除左右都有孩子的节点起个别名为d
2. 如果删除了58, 它既有左子树又有右子树, 我们应该找一个节点替代这个58的位置。我们这里找的是58的"后继节点"(就是离58元素最近的那个,
并且比58要大的节点)其实也就是59这个节点。如何找到59这个节点呢?(其实就是58的右子树中对应最小值的节点)
58右子树都比58大, 其中最小的那个元素就是比58大并且离58最近的元素。
3. 找到后继节点s, 即: s = min(d->right), s是d的后继
4. s->right = removeMin(d->right), 删除并返回了一个的树, 就会变为图2。
这里只挂载了右子树。
5. s->left = d->left把别名d的左子树挂载到后继节点s上,就形成图3了。
通过上面的步骤, d节点左右子树已经被后继节点s取代了, 这样就可以放心的删除节点d了。
图1: 41 图2: 41 图3: 41
\ \ \
58 59 59
/ \ => \ => / \
50 60 60 50 60
/ \ / \ \ / \ \
42 53 59 63 63 42 53 63
好了, 通过上面的学习, 了解了几种场景解决方式, 现在通过代码来看看如何解决。
public void remove(E e) {
root = remove(root, e);
}
private Node remove(Node node, E e) {
if (e.compareTo(node.e) == 0) {
// 第一种情况: 删除只有左孩子的节点(简单)
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 第二种情况: 删除只有右孩子的节点(简单)
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
/***
* 待删除节点左右子树都不为空的情况
*/
// 1. 找到比待删除节点大的最小节点, 即待删除节点右子树中最小的节点(找到后继节点)
// 2. 用后继节点顶替待删除节点的位置
Node succeed = minimum(node.right);
// 返回删除最小值后的一个新树, 最小值已经被我们记录住了, 然后设置左右子树
succeed.right = removeMin(node.right);
succeed.left = node.left;
// 这里之所以没有size--, 是因为removeMin方法已经做了
node.left = node.right = null;
return succeed;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(node.right, e);
return node;
} else {
node.left = remove(node.left, e);
return node;
}
}
