本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是LeetCode专题的第23篇文章。
今天来看一道很有意思的题,它的难度是Hard,并且有许多种解法。
首先我们来看题面,说是我们有若干个水坝,水坝的宽都是1,但是水坝的高度参差不齐。某一天我们向水坝围起来的部分灌水,一直到灌满为止,请问水坝中存储了多少单位的水?我们可以参考一下下图:
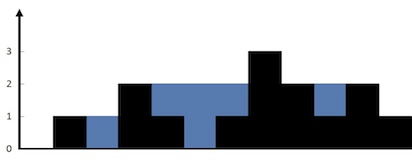
上图当中黑色的部分是水坝,蓝色的部分是存储的水。所有的水坝的宽度是1,长度是整数,不考虑损耗。
我们的输入是一个数组,表示若干个水坝的高度,要求的输出是一个整数,表示这些水坝围起来的面积。比如上图的样例为:
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
暴力
这题刚拿到手比较棘手,因为我们只知道水坝的高度,并不知道水坝围成了多少个区域,也不知道这些区域当中的形状是怎样的。
还是老规矩,我们先来思考暴力解法。在这题当中暴力解法可能不是非常明显,我们需要仔细分析一下上图当中的数据。
从上图样例当中我们可以看到,这些水坝由于高低不齐,会导致整个水坝中的水并不是一个整体,而是会被分成好几个部分。也就是说我们没办法直接求到结果,而需要对这些部分分别求水的体积,最后相加。
但是我们并不知道水坝中的水会被分成几个部分,所以直接求是不行的,那么有没有什么办法可以确定我们找到了一个完整的部分呢?
我们先把这个问题简化一下,在什么情况下水坝有存储水的能力呢?
如果水坝的高度递增行吗?那如果递减呢?
我们在纸上画一画很容易就想明白,递增和递减都不行,只有先递减再递增可以,也就是下图所示这样。
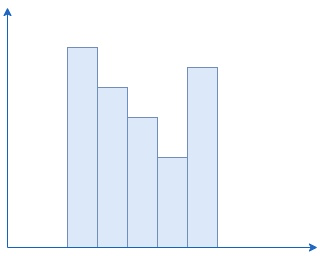
我们看下上图,水坝的高度先递减再递增,这样两边比较高的水坝就可以拦住一定体积的水。我们再思考一下,如果上图只是所有水坝的一部分,我们可以保证这个部分是完整的吗?显然应该不是,原因也很简单,因为水坝的右侧可能还会出现更高的水坝,如果出现了,那么整个部分的水平面还会提升,也就是说能存下更多的水,也就是下图的情况:
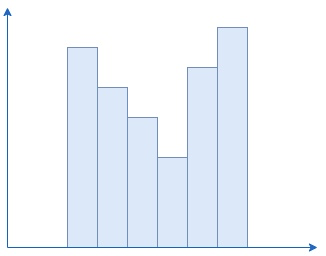
我们对照一下这两张图就可以想明白,当我们从左往右遍历的时候,只有遇到比最左侧的水坝更高的水坝的时候,这个部分才完整。想明白这点就容易了,我们从左往右遍历,维护一个局部最高值,当发现一个比局部最高值相等或更高的值的时候,就说明可以存储一部分的水,并且这部分水是完整的,我们来计算一下围成的水的面积。水的面积也很容易算,我们算出水平面的高度,然后减去水面下水坝的高度即可。
所以我们首先找到这样一个一个完整的水域,计算出每个水域的面积,最后将水域的总面积相加得到最终的结果。
思路是正确的,但是实现的时候会发现有点问题,什么问题呢?我们还拿上面的例子距离,你会发现当我们到达最高点了之后,后面的完整水域切分不出来了,因为没有比最高点更高的了。
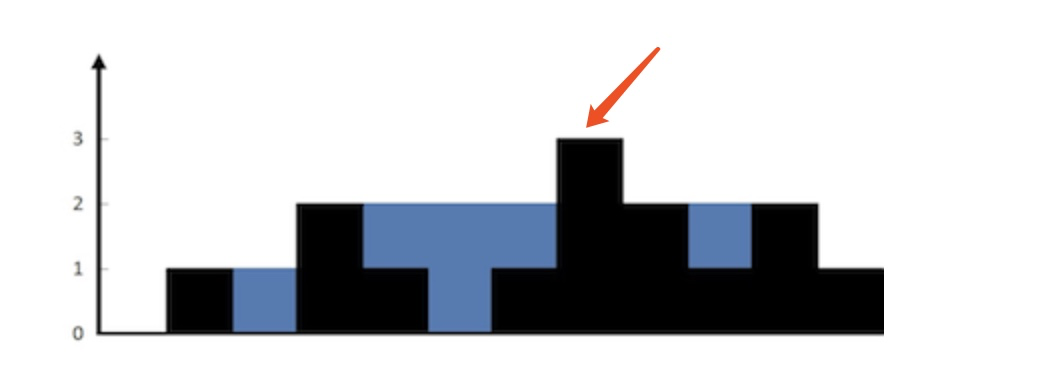
上图当中箭头标的位置是最高点,它的右侧再没有比它高的位置。我们是通过右侧出现大于或者等于它高度的水坝出现作为判断完整水域的条件,如果没有出现,我们就没办法判断究竟完整的水域能够延伸到哪里了。
这个问题比较棘手,我能想到最好的办法是将后面的部分翻转过来重复执行一次同样的操作。这是实现最简单代码最小的方法了。
我们试着写下代码:
class Solution:
# 从左往右遍历,找到大于当前最高点的水坝
# 计算这块水坝围成的面积
def solve(self, height):
n = len(height)
# 当前最高点和它的下标
fstHigh, fstIdx = 0, 0
ret = 0
for i in range(n):
# 如果找到,那么则遍历这个区域计算面积
if height[i] >= fstHigh:
# 水平线的高度就是左侧水坝的高度
# 也就是区域内的第二高度
waterHigh = fstHigh
for j in range(fstIdx, i):
ret += max(waterHigh - height[j], 0)
fstHigh, fstIdx = height[i], i
return ret, fstIdx
def trap(self, height: List[int]) -> int:
n = len(height)
# 先执行一次
ret, idx = self.solve(height)
# 如果右侧还有水坝剩余,则翻转再执行一次
if idx < n - 1:
# Python当中翻转整个数组的语法是[::-1]
# [n:-1:-1]不行,也就是第二个下标不能出现-1
if idx == 0:
cur, _ = self.solve(height[::-1])
# idx-1是为了把最高点的下标也包括进来
else:
cur, _ = self.solve(height[n-1:idx-1:-1])
ret += cur
return ret
当然也可以不用翻转,而是换成从右往左遍历,都是可以的。
two pointers
不知道大家理解了暴力解法之后,有没有一个想法,既然我们总可以找到一个最高的水坝(如果出现多个,则认为最右侧的那个最高),那么我们是不是可以根据这个最高的水坝的位置,将整个水库分成左右两个部分,然后从左右两个边界朝着中间收缩呢?
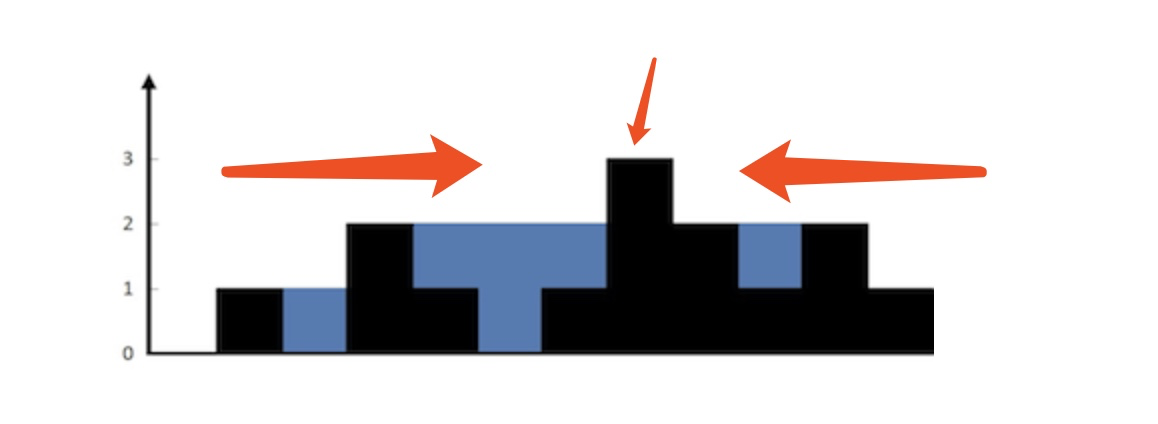
也就是说用和刚才一样的方法划分完整的水域,只不过我们用两个指针从两边一起遍历,一个指针从左往右,另一个指针从右往左。还是一样,当碰到大于等于目前最大值的时候认为是一个完整的水域,计算面积。
似乎这种方法和上面的一样,但其实不然,仔细分析可以发现一个优化的点。
在之前的方法当中,我们并不确定我们从左往右一定可以找到比目前最大值更大的值。很有可能之前找到的最大值就是全局最大的,后面不会有更大的值出现。所以我们必须要等更大的值出现之后才能计算水域的面积。
而两个指针的方法当中,我们每次移动其中较小的那个,这样我们可以保证两个指针相遇的位置就是全局最大值。既然我们可以保证两个指针会相遇在全局最大值,那么移动指针的时候就可以保证后面一定还会有更高的位置出现,那么我们就没必要等找到更大的值之后再计算水域面积了,就可以在当下直接计算了。
我们来看个例子:
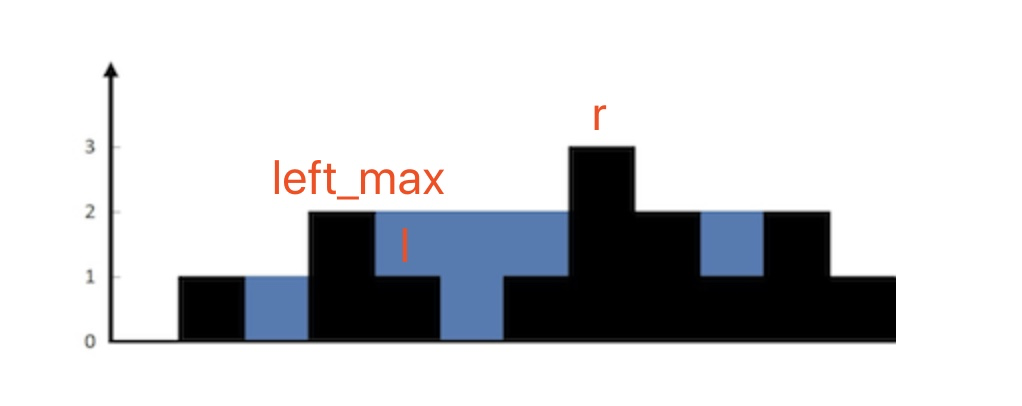
在上图的例子当中,r指针的高度是3,大于目前的l,我们需要移动指针l,目前左边遇见的最大值是2。由于l和r没有相遇,所以我们可以保证l的右侧一定还有大于left_max的高度出现,否则该移动的就是r了。所以我们可以保证,left_max之后一定可以构成一个水域,并且这个水域的高度就是left_max。于是我们可以直接计算当前水坝贡献的水域面积,就是left_max - height[l]就等于1.
在这个算法当中,我们控制两个指针移动,当两个指针相遇的时候则结束。可以想明白,我们一共移动了n次,所以这是一个的算法,我们来看下代码里的细节:
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
l, r = 0, n-1
# 用两个变量分别记录左边和右边的最大值
lmax, rmax = 0, 0
ret = 0
while l < r:
# 移动高度较小的指针
if height[l] < height[r]:
# 如果超过左边最大值,则更新
if height[l] > lmax:
lmax = height[l]
# 否则累加当前水坝贡献的面积
else:
ret += lmax - height[l]
l += 1
else:
# 同理
if height[r] > rmax:
rmax = height[r]
else:
ret += rmax - height[r]
r -= 1
return ret
和上面的代码相比,这段代码要简明很多,看起来也更顺眼。虽然代码简单,但是能把其中的门道想明白并不容易,如果有觉得迷糊的同学可以结合上面的图片再思考思考,举例子作图是思考算法各种情况的王道,这个办法大家一定要掌握。
构造法
如果真的理解了上面的解法会发现上面的解法本质上是将水域进行纵向切分,然后每一块单独累加来计算总面积的,也就是这样:
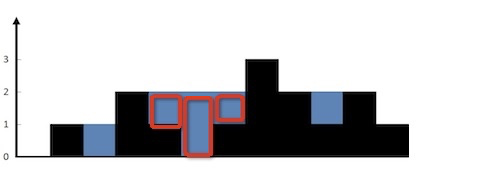
既然本质都是切分,那么我们能不能不搞那么多花哨的操作直接进行切分呢?当然是可以的,难点只有一个,就是我们需要知道当前的水平面的高度,这个是核心问题。我们之前搞那么多高度比来比去本质也是为了求水平面的高度。
那么有没有什么办法可以直接求到水平面的高度呢?其实是有的,方法很简单也很粗暴。我们分析一下上图,可以发现,对于未知i来说,它的水平面高度是由两个水坝决定的。也就是i两边最高的水坝。
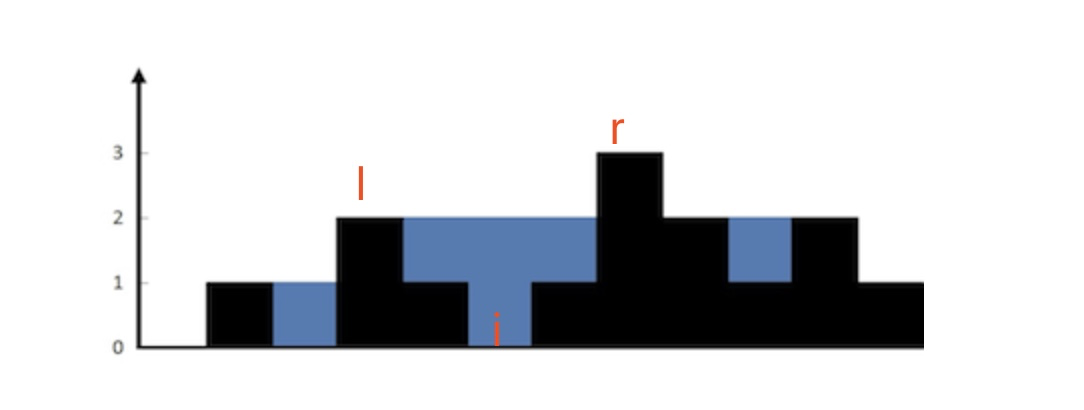
比如对于上图的例子来说,i位置的水平面高度是由它左侧最高的l和右侧最高的r其中较小的那个高度决定的。我们并不关心l和r的下标是多少,我们只关心它的高度。既然如此,我们把所有i左右两侧最高的高度记录下来不就行了?
我相信如果你是自己想到的这个方法,在你想通的那一刻,你一定会觉得自己实在是太机智了。
道理想明白了,编码完全没有难度,我们随手就来:
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
if n == 0:
return 0
ret = 0
lmax = [0 for _ in range(n)]
rmax = [0 for _ in range(n)]
lmax[0] = height[0]
# 存储小于等于i的最大值
for i in range(1, n):
lmax[i] = max(lmax[i-1], height[i])
rmax[n-1] = height[n-1]
# 存储大于等于i的最大值
for i in range(n-2, -1, -1):
rmax[i] = max(rmax[i+1], height[i])
for i in range(n):
cur = min(lmax[i], rmax[i])
ret += max(0, cur - height[i])
return ret
这个算法同样是的复杂度,但是实现起来比上面的还要简单。虽然我们单纯看解法它简单得难以置信,但是能够想到这个简单的解法并不容易,除了需要我们充分理解题意之外,更需要我们有一定的解题技巧和思维灵敏度。
最后,我们来看本篇文章的大菜,也是本题的最后一个经典解法——单调栈
单调栈
在我们介绍具体的算法之前,我们先来看一下单调栈这个数据结构。严格说起来它并不是新的数据结构,只是栈的简单变种。
顾名思义,单调栈即栈的元素都是单调的,或者单调递增或者单调递减。由于栈先进后出的特性,显然我们是不能对栈内的元素排序的。我们只能通过弹出来保证栈内元素的有序性,也就是说我们是通过抛弃一些数据来达到有序的,而不是排序。
举个例子,比如说目前栈内的数据是[3, 7, 10]递增排列,栈顶的位置是10。如果我们需要插入16,由于它大于10,所以我们可以直接插入栈顶,栈会变成[3, 7, 10, 16]。如果我们要插入的元素是8,由于它小于10,所以我们会弹出栈顶的10,接着和7比较,发现它大于7,那么插入,得到[3, 7, 8]。也就是说通过单调栈我们可以保证栈内的元素是有序的,以及栈顶的元素是最大或者最小的。
利用这两个性质,我们可以解决很多问题。
我们先把单调栈放一边,先回到问题的分析。之前的解法都是纵向切割的水域面积,我们能不能横向切割呢?就像这样:
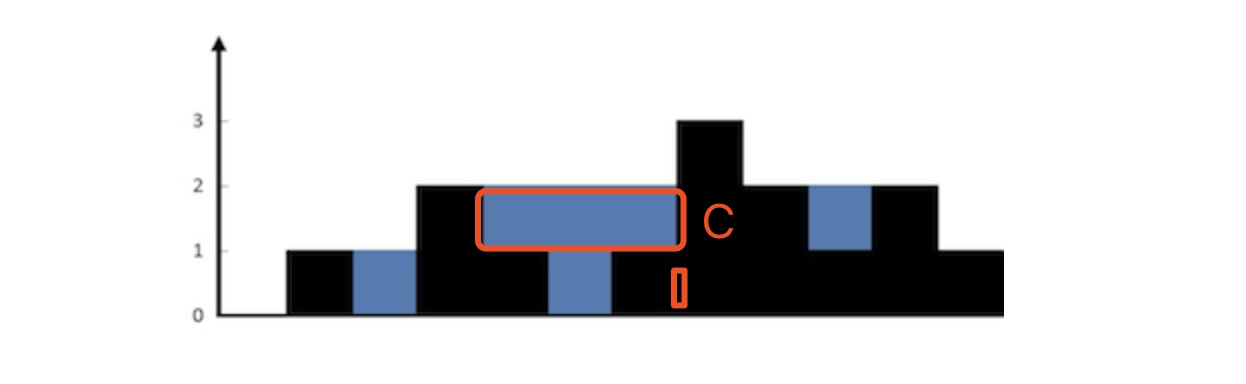
红框的内容表示以C水坝为右侧挡板构成的面积。
C隔成的面积分为两块,一块面积是0,一块的面积是3。面积是0的很好理解,因为宽度为0,面积是3,是因为横截出来的面积高度是1,宽是3。宽度3很好理解,这里的高度1是通过下图当中水坝A和水坝B的高度差值得到的,如下图:
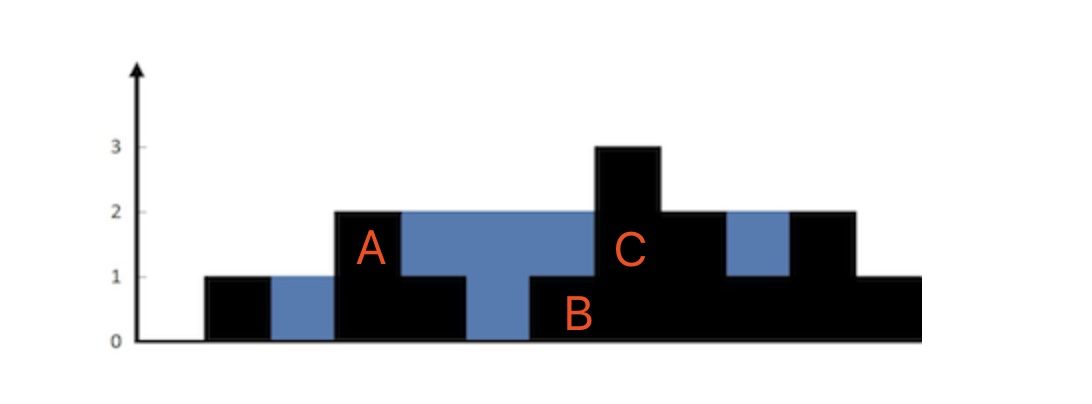
这一切的基点是水坝C,对于水坝C来说,B是离它最近并且最小的,A是次小的。所以它和A隔出的水域的高度是水坝A和B的高度差,而不是A和C的,我想这点应该不难理解。
那么,我们需要一个数据结构维护C之前水坝的高度情况,并且需要这个数据结构里的元素是递增的。另外,当我们计算完C作为右侧挡板形成的面积之后,由于C的出现挡住了它之前所有比它矮的水坝,所以我们需要移除数据结构当中小于C的所有内容。
也就是说我们需要数据结构有序,并且需要抛弃小于当前元素的数据。那么显然用单调栈就非常合适。我们在读入C的高度的时候,先弹出B的下标,我们计算它和C之间的水域面积,再弹出A,我们同样计算面积,一直到栈空或者栈顶的元素大于C即可,这时候我们插入C。
对于所有的位置,我们都可以重复以上的操作,我们只需要将隔成的面积累加起来即可。我们可以看下代码,获取更多细节,虽然这个算法看起来麻烦,但是落在代码上并不复杂:
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
if n == 0:
return 0
ret = 0
# 单调栈,我们存储的是下标
stack = []
for i in range(n):
# 弹出栈顶小于当前元素的元素
while len(stack) > 0 and height[stack[-1]] < height[i]:
idx = stack.pop()
if len(stack) == 0:
break
# 水域的宽,即下标差值-1
l = i - stack[-1] - 1
# 水域的高为当前栈顶的值减去之前栈顶的值
ret += l * (min(height[stack[-1]], height[i]) - height[idx])
stack.append(i)
return ret
光看代码可能会觉得有一点绕,我们需要结合一下上面的图,仔细推导一下过程。由于单调栈并没有涉及元素的排序,并且所有的元素最多只会进栈和出栈一次,所以这也是一个的算法。但是相比之下,它的常数要比上面介绍的几种要大一些。
今天的文章就是这些,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。
