01 按既定顺序创建目标数组
题目描述【Easy】
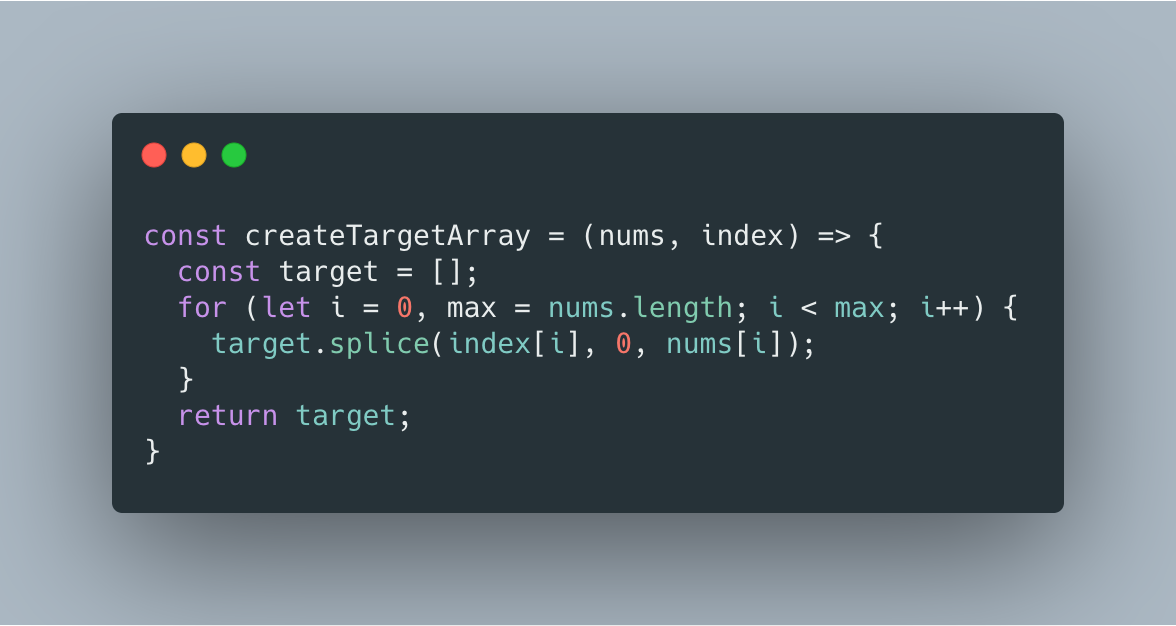
给你两个整数数组 nums 和 index。你需要按照以下规则创建目标数组: 目标数组 target 最初为空。 按从左到右的顺序依次读取 nums[i] 和 index[i],在 target 数组中的下标 index[i] 处插入值 nums[i] 。 重复上一步,直到在 nums 和 index 中都没有要读取的元素。 请你返回目标数组。 题目保证数字插入位置总是存在。 示例: 输入:nums = [0,1,2,3,4], index = [0,1,2,2,1] 输出:[0,4,1,3,2] 解释: nums index target 0 0 [0] 1 1 [0,1] 2 2 [0,1,2] 3 2 [0,1,3,2] 4 1 [0,4,1,3,2]
本道题考察数组的基本操作。
02 5178.四因数
题目描述【Medium】
给你一个整数数组 nums,请你返回该数组中恰有四个因数的这些整数的各因数之和。 如果数组中不存在满足题意的整数,则返回 0 。 示例: 输入:nums = [21,4,7] 输出:32 解释: 21 有 4 个因数:1, 3, 7, 21 4 有 3 个因数:1, 2, 4 7 有 2 个因数:1, 7 答案仅为 21 的所有因数的和。
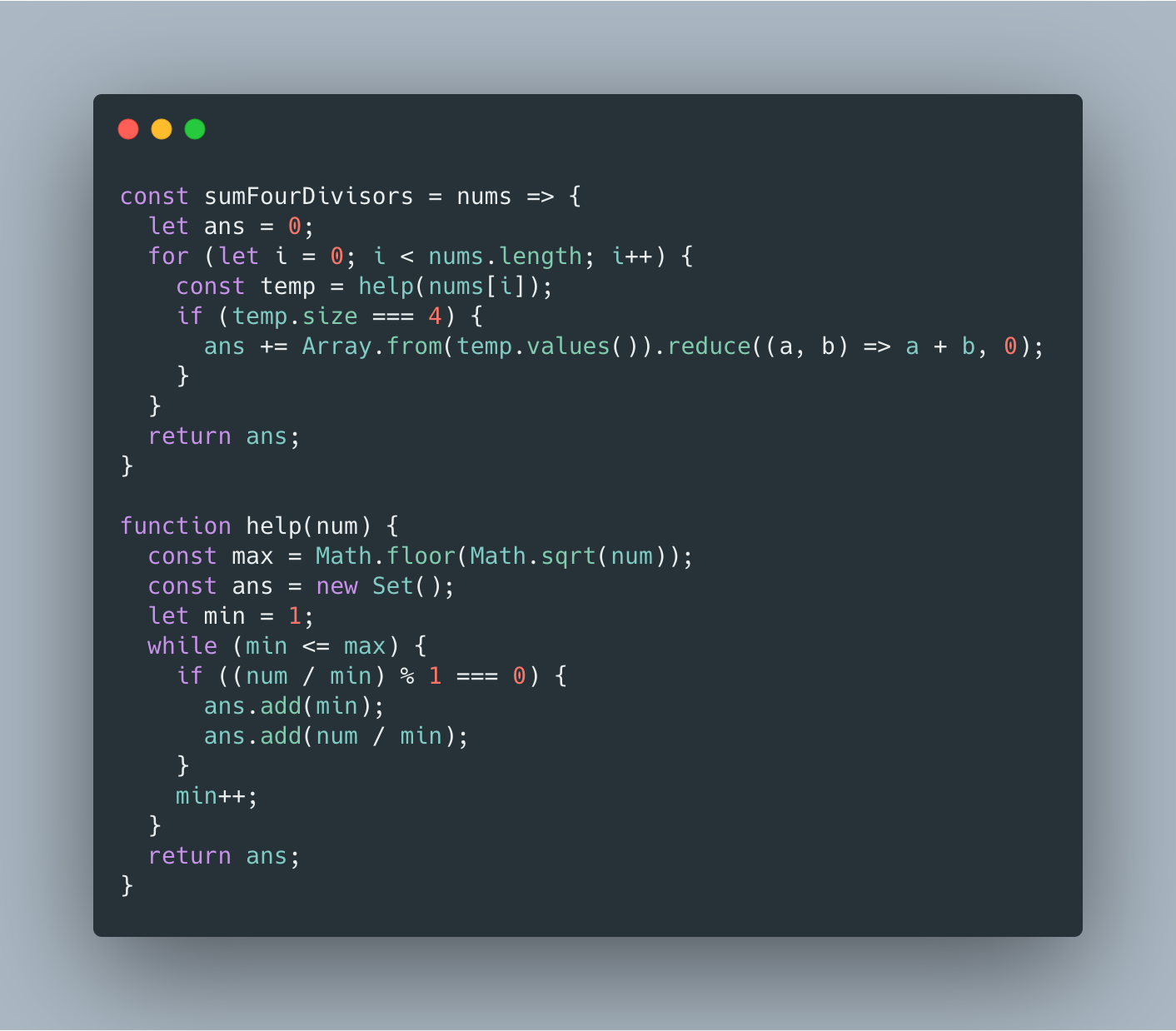
本道题主要考察以下两点:
利用 JavaScript 中的 Set 数据结构去重
利用开方操作减少不必要的循环次数
03 检查网格中有效路径
题目描述【Medium】
给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是: 1 表示连接左单元格和右单元格的街道。 2 表示连接上单元格和下单元格的街道。 3 表示连接左单元格和下单元格的街道。 4 表示连接右单元格和下单元格的街道。 5 表示连接左单元格和上单元格的街道。 6 表示连接右单元格和上单元格的街道。 示例: 输入:grid = [[2,4,3],[6,5,2]] 输出:true 解释:如图所示,你可以从 (0, 0) 开始,访问网格中的所有单元格并到达 (m - 1, n - 1) 。
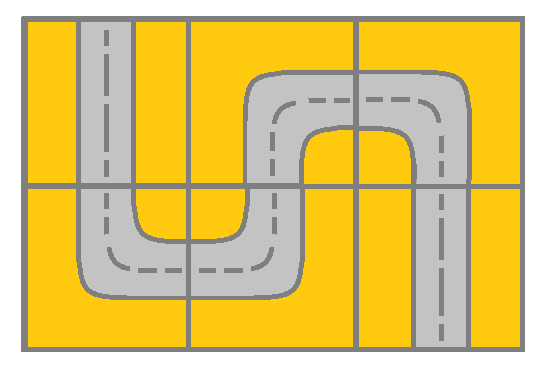
本道题主要考察图论中的搜索算法。
在决定使用哪种搜索方法之前,需要先梳理一下这个寻路的方法。
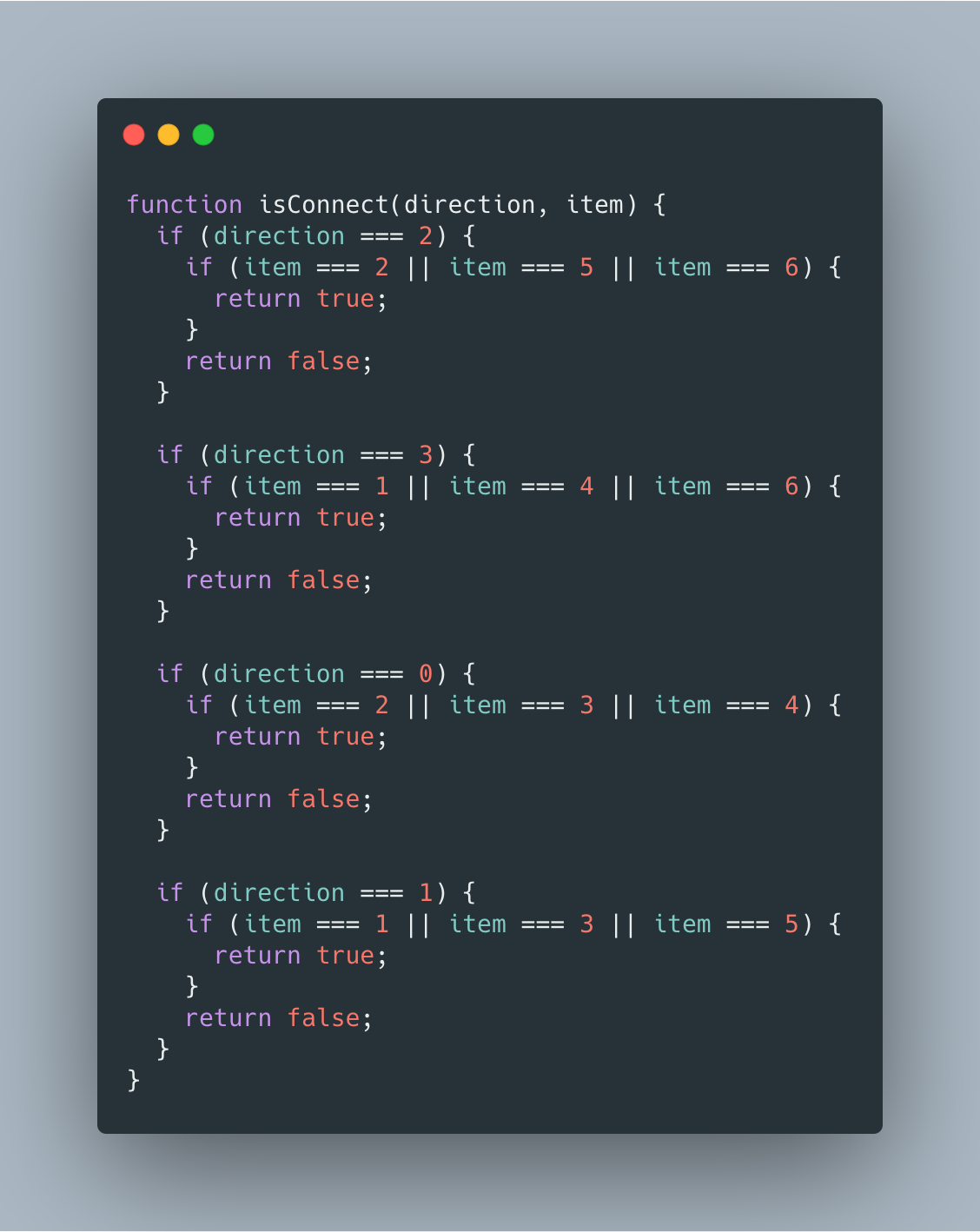
首先对于任意一个街,需要知道它可以往哪几个方向(上右下左)移动:
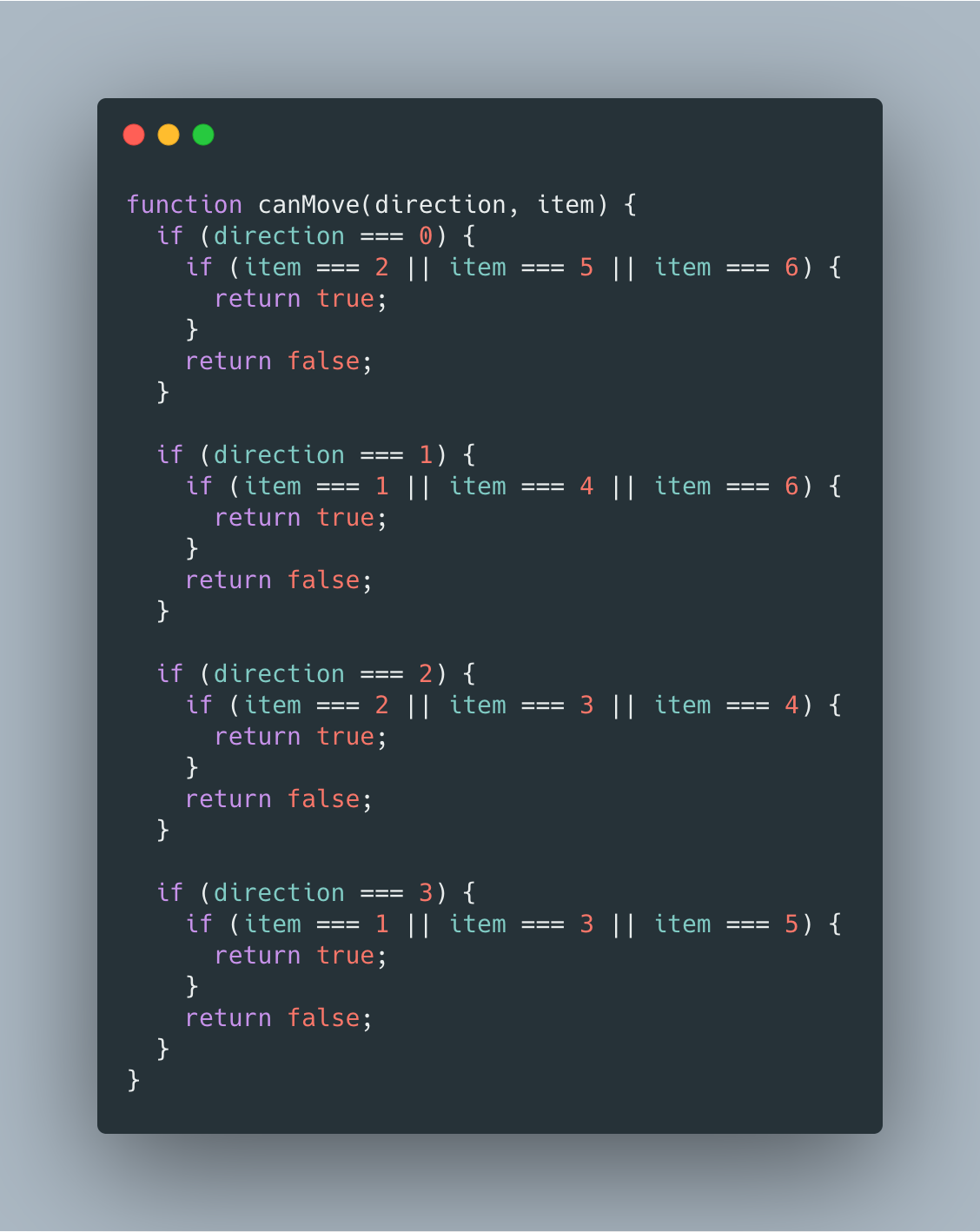
接下来还需要判断下一个街道与当前街道是否具有连通性:
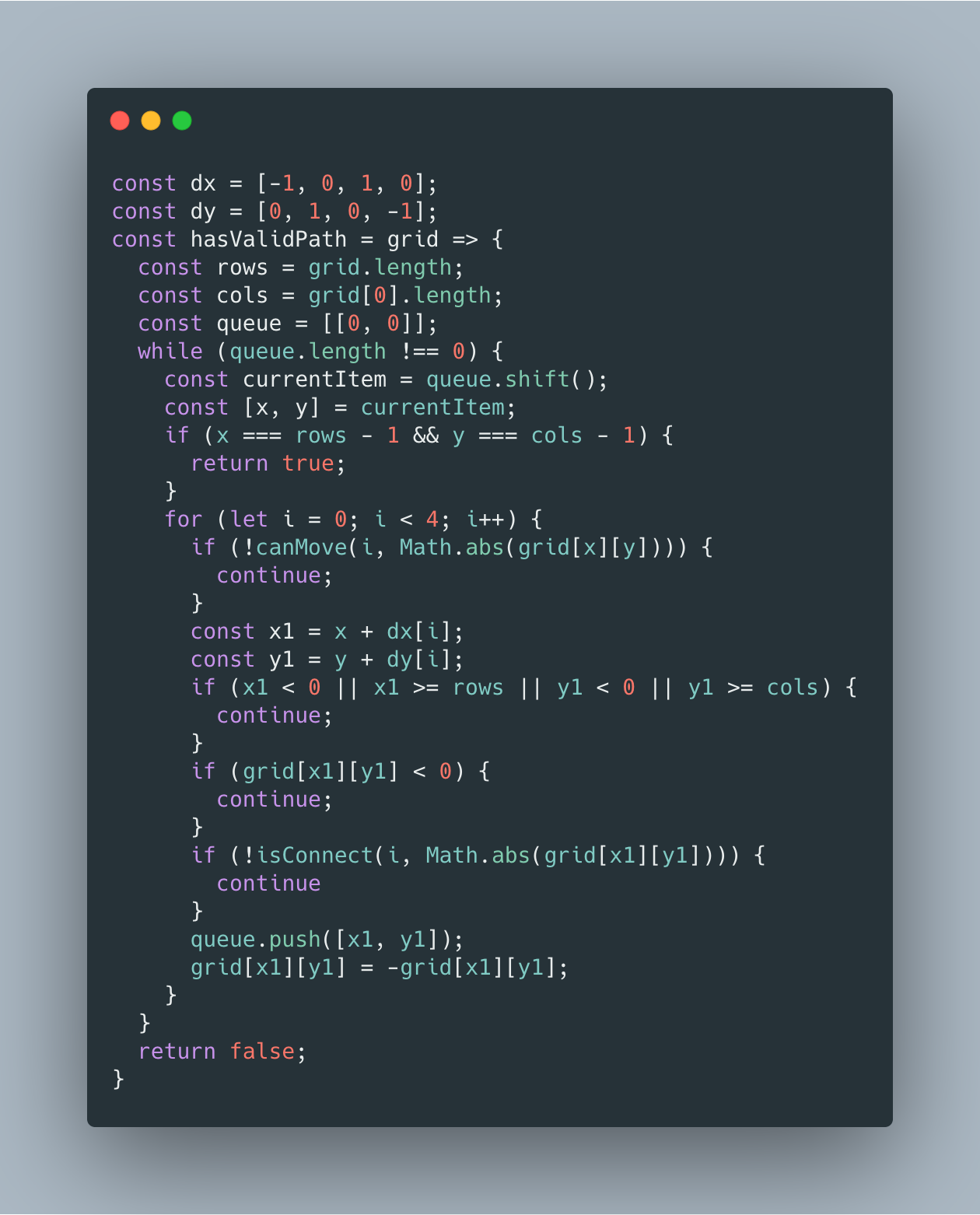
很遗憾本道题采用 DFS 会在最后几个测试用例中出现爆栈情况,所以这里介绍 BFS 的写法,在搜索的过程中需要细节拉满:
判断当前街道可以往哪几个方向移动
判断下一个街道是否超出边界
判断下一个街道是否已经访问过,这里可以通过将原值置为负数,从而节省记录状态所需的额外空间
判断当前街道与下一个街道是否连通
04 1392.最长快乐前缀
题目描述【Hard】
「快乐前缀」是在原字符串中既是 非空 前缀也是后缀(不包括原字符串自身)的字符串。 给你一个字符串 s,请你返回它的 最长快乐前缀。 如果不存在满足题意的前缀,则返回一个空字符串。 示例: 输入:s = 'level' 输出:'l' 解释:不包括 s 自己,一共有 4 个前缀('l', 'le', 'lev', 'leve')和 4 个后缀('l', 'el', 'vel', 'evel')。最长的既是前缀也是后缀的字符串是 'l' 。
这是一道 Hard 难度的题目,但是当我暴力求解 AC 之后,我的内心是这样的:

抛开暴力求解的快乐,本道题可以利用双指针技巧求解字符串的部分匹配表。
这个名词是不是很熟悉,没错就是 KMP 字符串匹配算法中的部分匹配表(最大公共前后缀数组)。
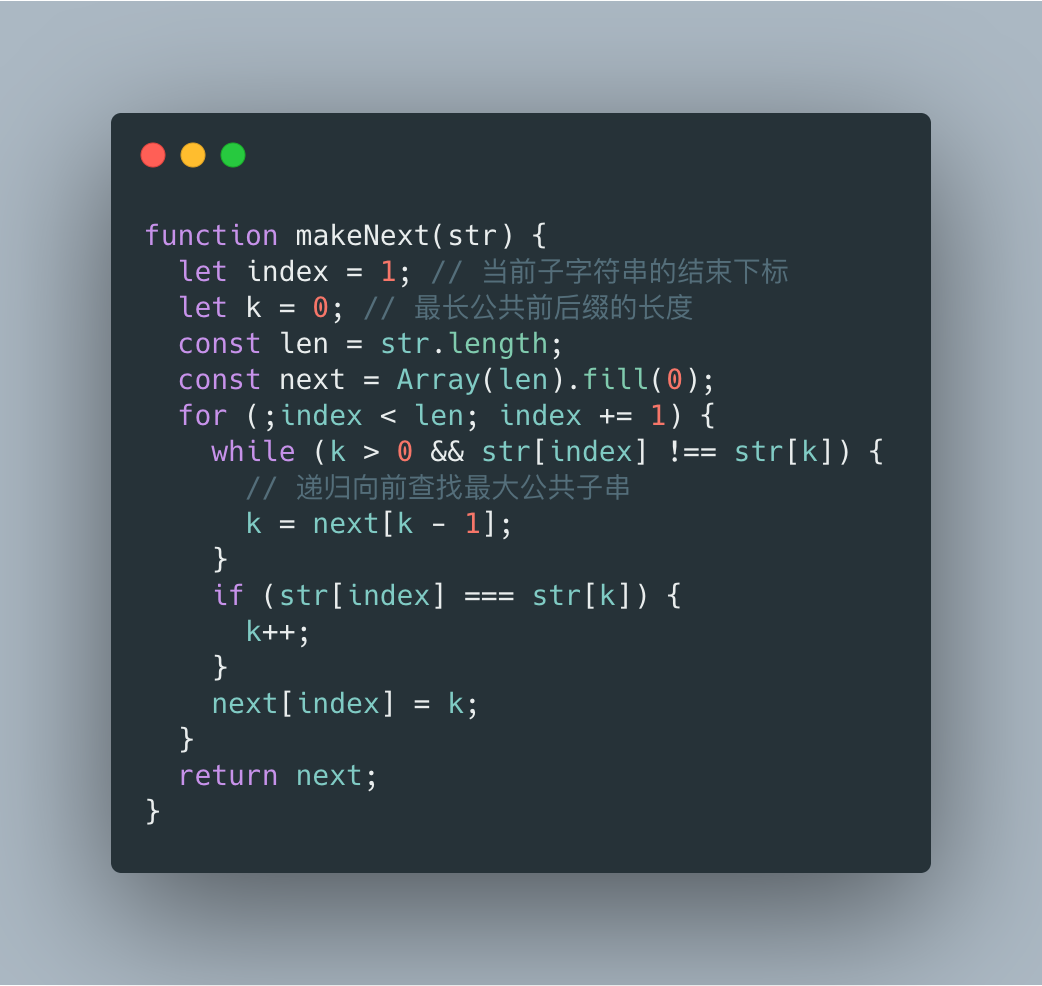
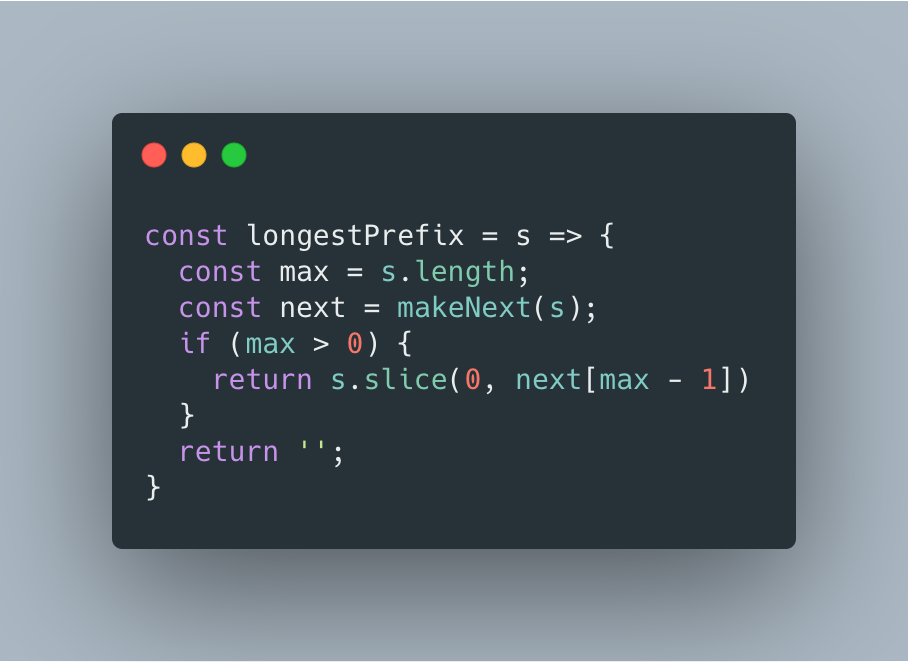
有了部分匹配表之后,就可以知道整个字符串的最长公共前后缀的长度,即可求出最快乐前缀。
05 往期精彩回顾
