- 本文首发自公众号:RAIS
前言
本系列文章为 《Deep Learning》 读书笔记,可以参看原书一起阅读,效果更佳。
估计
统计的目的是为了推断,大量的统计是为了更好的推断,这就是一种估计,一种根据现有信息对可能性的一种猜测。
- 点估计:点估计指的是用样本数据估计总体的参数,估计的结果是一个点的数值,因此叫做点估计。这个定义非常宽泛,
,其中几乎对 g 没有什么限制,只是说比较好的 g 会接近真实的 θ。
- 函数估计:是一种映射关系,如
,其中 ϵ 是从 x 中预测不出来的,我们不关心,我们关心的是函数估计 f,函数估计是一种从输入到输出的映射关系。
偏差
估计的偏差定义为:,这很好理解,估计与实际值之间的距离就是偏差,如果偏差为 0,则
是
的无偏估计,如果在 m 趋近于无穷大时,偏差趋近于 0,则
是
的渐进无偏。
方差
上面我们用估计量的期望来计算偏差,我们还可以用估计量的方差度量估计的变化程度,我们希望期望这两个值都较小。
对于高斯分布来说,我们有:
- 样本均值
是高斯均值参数 μ 的无偏估计;
- 样本方差
是
的有偏估计;
- 无偏样本方差
是
的无偏估计;
无偏样本方差显然是比较不错的,但是并不总是最好的,有时候某一些有偏估计也是很好的。比如在机器学习中,均值标准差就非常有用:
或者写成
均方误差(MSE)
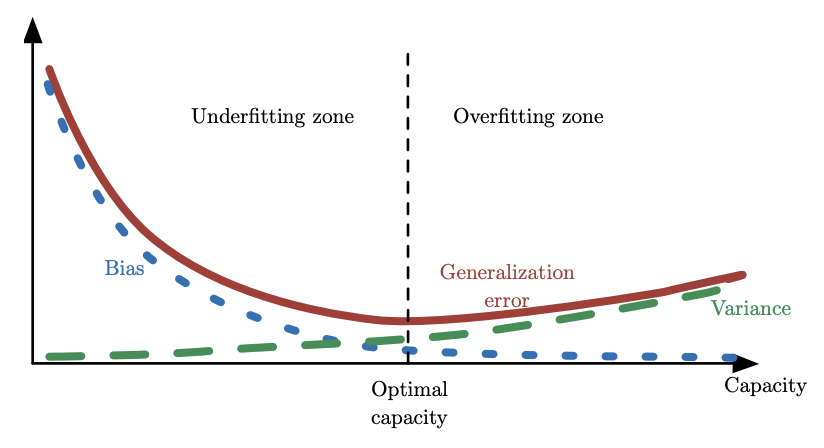
鱼和熊掌不可得兼,偏差和方差度量着估计量的两个不同误差来源,偏差度量着偏离真实函数或参数的误差,方差度量着数据上任意特定采样可能导致的估计期望的偏差,两个估计,一个偏差大,一个方差大,怎么选择?选择 MSE 较小的,因为 MSE 是用来度量泛化误差的。偏差和方差之和就是均方误差:
总结
本篇主要介绍了估计、偏差和方差,可以用来正式的刻画过拟合。
- 本文首发自公众号:RAIS