前言
归并排序与堆排序的时间复杂度都为O(nlogn),这两种算法的应用场景较为广泛,本文采用图文形式详细讲解归并排序的实现思路,并用JavaScript将其实现,欢迎各位感兴趣的前端开发者阅读本文。
概念
归并排序算法会将序列分成长度相同的两个子序列,当无法继续往下分时(每个子序列都只有一个数据时),就对子序列进行归并。
归并是指把两个排序好的子序列,合并成一个有序序列。该操作会一直重复执行,直到所有子序列都归并为一个整体为止。
归并图解示例
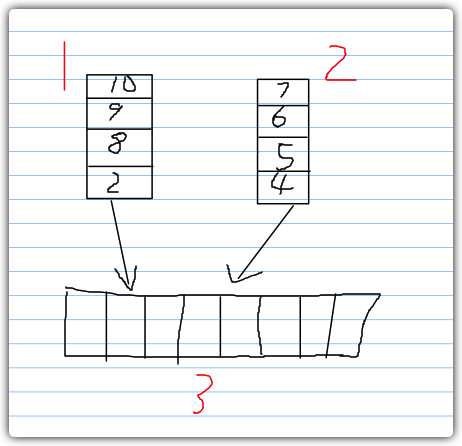
如图所示,有两个已经排好序的数组1和2,我们把1号数组和2号数组的内容,按照从小到达的顺序放进3号数组里,即为归并操作,接下来就跟大家分享下如何进行归并操作。
- 如图所示,我们先将1号数组和2号数组的内容放进3号数组里
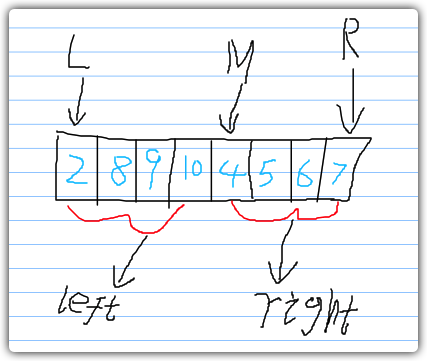
我们将1号数组区域标为left,将2号数组区域标为right,3号数组最左端的元素我们用L表示,3号数组最右端的元素我们用R表示,求出3号数组的中间值后我们用M表示。
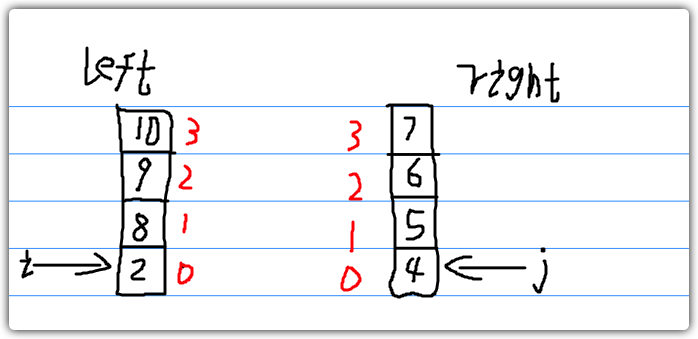
- 如图所示,我么将数组拆分为两个小数组,left和right,用i指向left数组的0号元素,用j指向right数组的0号元素
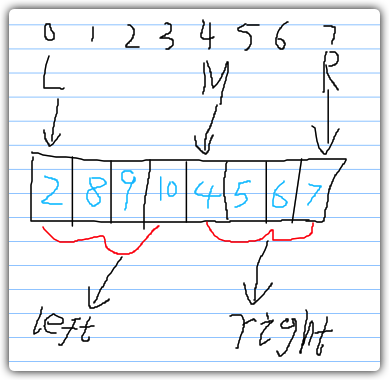
如图所示,我们已知M的位置,则左边数组的大小为M - L,右边数组大小为R - M + 1,计算出左、右数组的大小后,我们对数组进行填充。
数组的填充规则为: 左数组:从L开始到M结束,右数组: 从M开始到R结束。
如图所示,我们分别用i、j、k三个字母指向左、右数组的0号元素、合并后的数组的0号元素。
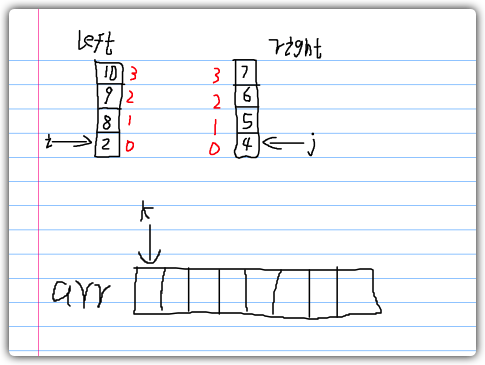
如图所示,我们用左数组的0号元素和右数组的0号元素进行大小比较,将小的一方放进arr数组的k号位置,k移动至下一个位置。
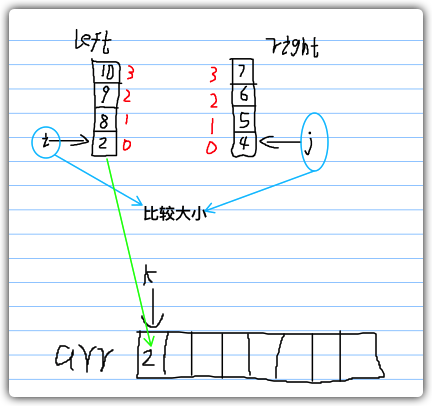
如图所示,i号元素已经放入数组中,此时我们将i移动到下一个位置,将其与j进行大小比较,将小的一方放进arr数组中,k移动至下一个位置。
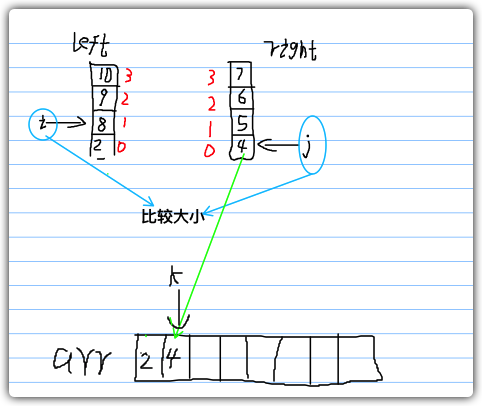
如图所示,j号元素已经放入数组中,此时我们将j移动到下一个位置,将其与i进行大小比较,将小的一方放进arr数组中,k移动至下一个位置。
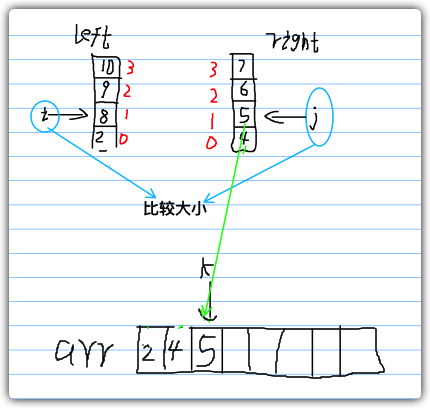
重复,上述操作,直至一方数组全部都取完
如图所示,right数组的数据已被全部取出
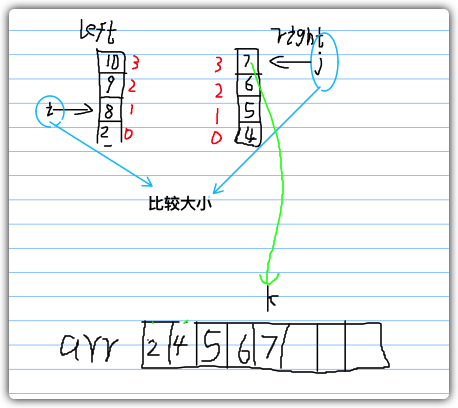
若一方数组的数据被全取出后,直接将另一方数组中的元素放进arr数组即可。
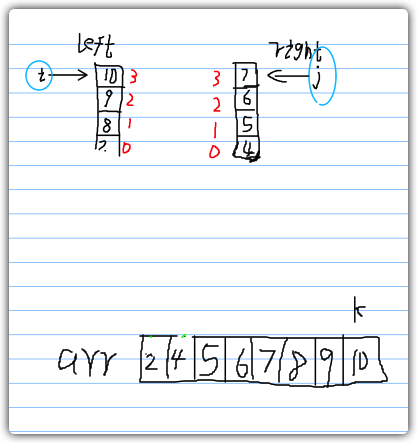
归并排序图解示例
上述的归并操作,是将已经排序好的两组数据归并成一个数组,然后进行排序,正常情况下,我们传入的数组是乱序的,我们会把数组从中间分开,分为左和右,然后想办法让两方的数据按照从小到达进行排序,然后合并两方的数据,则排序完成。
例如,我们要将下方数据进行归并排序。

-
将序列对半分割(2段)
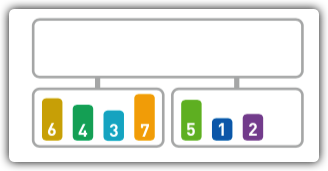
-
在继续往下分
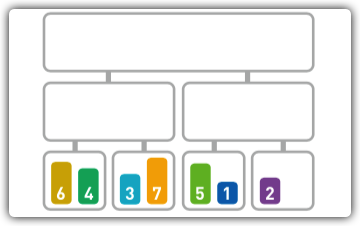
-
分割完毕,结下来对分割后的元素进行合并
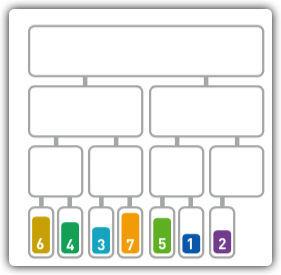
-
将6与4进行合并,合并后的顺序为[4,6]
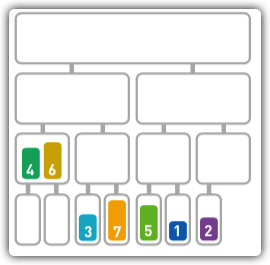
-
接下来把3和7进行合并,合并后的顺序为[3,7]
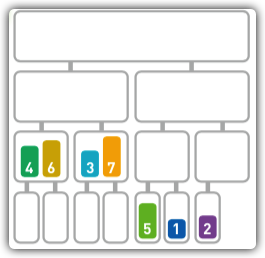
-
此时,我们产生了两组从小到大排列的数据,符合了归并的要求,我们将这两组数据代归并中,进行合并。
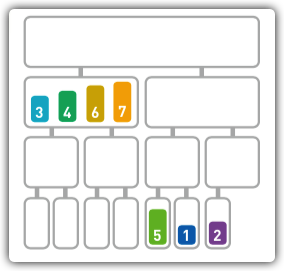
-
此时,我们发现还剩余两组数据未进行排序,我们递归上述操作,将这两组数据进行合并
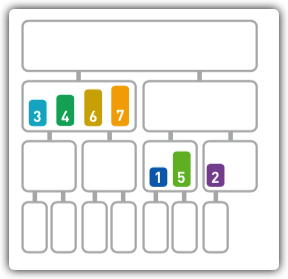
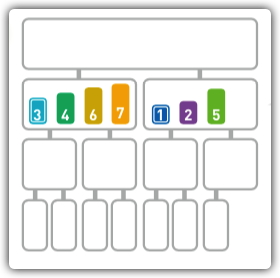
-
合并完后,我们发现又剩余两组数据,符合了归并的要求,我们继续调用归并,将这两组数据进行合并,排序完成。
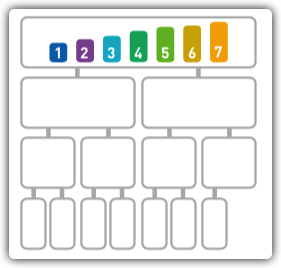
用JS实现归并排序
归并的实现
正如归并图解所描述,要实现两个数组的合并,前提是两组数据中的数据已经排列按照从小到大的顺序进行排列。
-
声明归并函数:
- 参数arr为两组从小到大排序的数组,将其合并成一个以后的数组。
- 参数L为数组的起点索引
- 参数M为数组的中间点(分割点),用于标识两组从小到大排序的数组,M左边的数据为一个数组(leftArr),M本身以及它右边的数据为一个数组(rightArr)。
- 参数R为数组的终点索引
-
分别计算左、右数组的长度
- 左边数组的长度为M - L
- 右边数组的长度为R - M + 1
-
声明左、右数组,初始化其长度
-
根据中间值,分别将arr中的数据填充到左、右数组
- 左数组: 从L填充到M(不包含M)
- 右数组: 从M(包含M)填充到R
-
将两组数据进行合并(从小到大进行排序)
-
声明3个变量:i, j, k
- i指向左侧数组的每一项
- j指向右侧数组的每一项
- k指向合并后的数组的每一项
-
将左侧数组的每一项数据与右侧数组的每一项数据进行大小比较
- 当前遍历到左侧数组的数据 < 当前遍历到的右侧数组的数据,则arr的k项为当前左侧数组的数据。i自增,k自增。
- 当前遍历到左侧数组的数据 > 当前遍历到的右侧数组的数据,则arr的k项为当前右侧数组的数据。j自增,k自增。
-
判断左、右数组是否比较完成
- 如果左侧数组的数据已经比较完,右侧数组的数据还未比较完,则arr的k项就为右侧数组的剩余项。
- 如果右侧数组的数据已经比较完,左侧数组的数据还未比较完,则arr的k项就为左侧数组的剩余项。
-
接下来,我们将上述思路用代码实现:
/**
* 归并函数
* @param arr
* @param L 数组的起点
* @param M 数组的分割点
* @param R 数组的终点
*/
const merger = function (arr, L, M, R) {
// 左边数组大小和右边数组大小
let left_size = M - L;
let right_size = R - M + 1;
// 声明左边数组和右边数组
let leftArr = new Array(left_size);
let rightArr = new Array(right_size);
let i,j,k;
// 填充左数组(从L开始到M结束)
for (i = L; i < M; i++){
leftArr[i-L] = arr[i];
}
// 填充右数组(从M开始到R结束)
for (i = M; i <= R; i++){
rightArr[i-M] = arr[i];
}
// 数组合并
i = 0; j = 0; k = L;
while (i < left_size && j < right_size){
// 如果左边数组的i项小于右边数组的j项,则数组的k项就为左边数组的i项。否则数组的k项就为右边数组的j项
if(leftArr[i] < rightArr[j]){
arr[k] = leftArr[i];
i++;
k++;
}else{
arr[k] = rightArr[j];
j++;
k++;
}
}
// 当右边数组到顶部后,左边数组还未到顶部,则将剩余元素放进arr中
while (i < left_size){
arr[k] = leftArr[i];
i++;
k++
}
// 当左边数组到顶部后,右边数组还未到顶部,则将剩余元素放进arr中
while (j < right_size){
arr[k] = rightArr[j];
j++;
k++;
}
};
- 测试下我们写的归并函数
const dataArr = [2,8,9,10,4,5,6,7];
/*测试合并*/
merger(dataArr,0,4,7);
// 合并后的数据
console.log(dataArr);
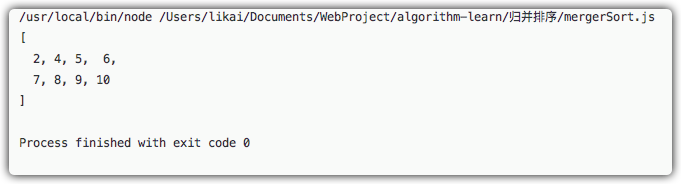
归并排序的实现
实现归并排序,我们首先需要计算出数组的中间值,然后将乱序的数组进行分割(分割到无法继续分割位置),分割完毕后,将分割的两组数据进行合并,递归操作即可完成归并排序。
- 计算中间值: (L + R) / 2
- 分割左、右数组
- 合并分割后的数据
- 递归操作(直至L = R)
接下来,我们看下代码的实现:
const mergerSort = function (arr,L,R) {
if(L===R){
// 数据已经切割完毕
return false;
}
else{
// 计算中间值(向下取整)
let M = Math.floor((L + R) / 2);
// 分割后,把左边的数据进行一次归并排序
mergerSort(arr,L,M);
// 对右边的数据进行一次归并排序
mergerSort(arr,M+1,R);
// 合并两边的数据
merger(arr,L,M+1,R)
}
};
- 测试下我们写的归并排序
const dataArr = [6,4,3,7,5,1,2];
/*测试排序*/
mergerSort(dataArr,0,dataArr.length - 1);
// 合并后的数据
console.log(dataArr);
写在最后
- 文中使用的图片源自《我的第一本算法书》,如若侵权,请评论区留言,作者立即删除相关图片。
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于掘金,未经许可禁止转载💌