一、栈
1.1 栈的特性
先进后出
1.2 栈结构
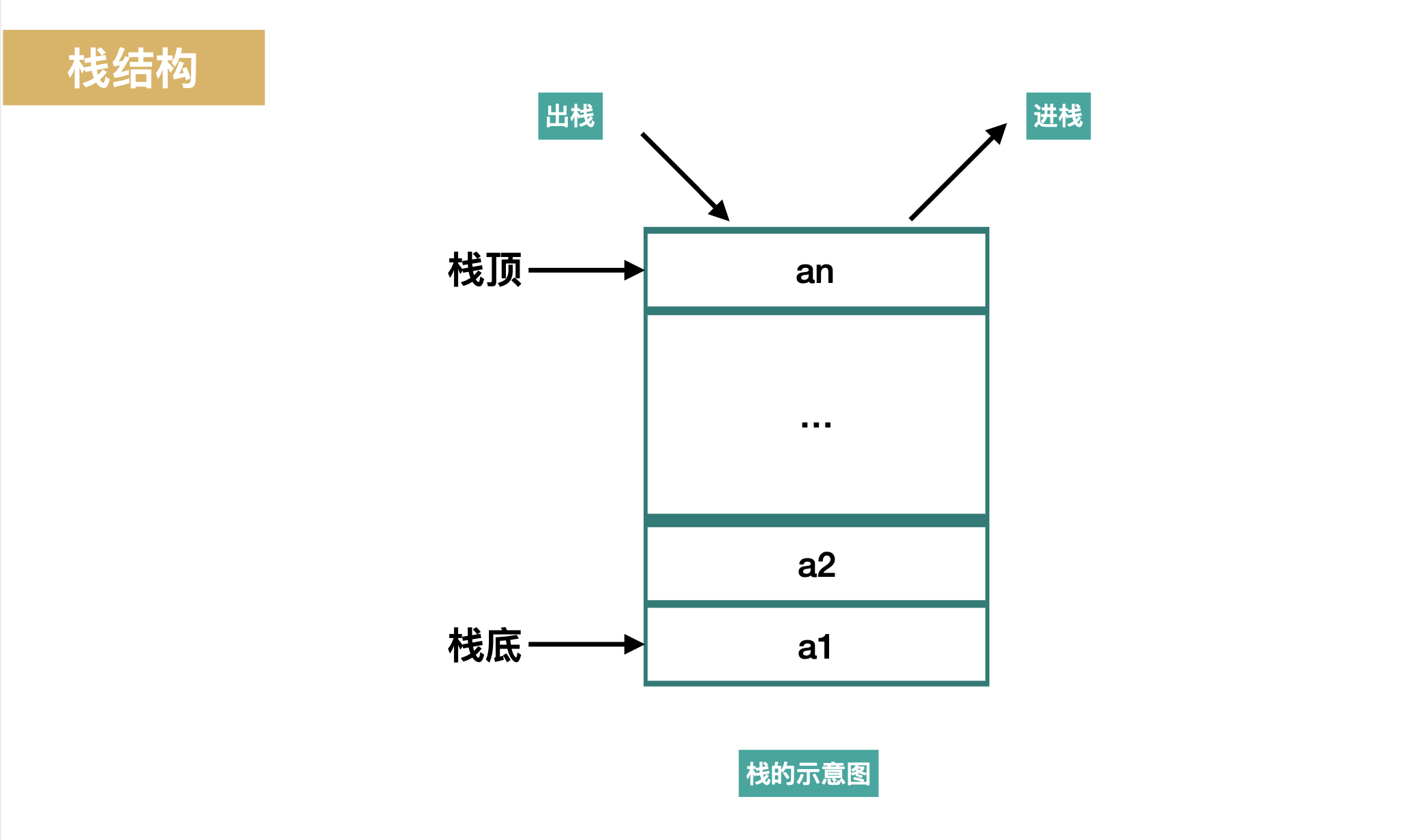
- 栈顶和栈底的两个指针,分别指向最后一个入栈的数据和最先入栈的数据
- 出栈和入栈都是从栈顶的数据开始,只移动栈的指针执行指向,这就是一个栈结构
话不多说,采用顺序存储和链式存储分别来实现一下栈结构
1.3 栈 - 顺序栈实现
1.3.1 顺序栈结构及初始化
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;
typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int */
/* 顺序栈结构 */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* 用于栈顶指针 */
}SqStack;
//4.1 构建一个空栈S
Status InitStack(SqStack *S){
S->top = -1;
return OK;
}
1.3.2 顺序栈入栈
算法实现:
// 插入元素e为新栈顶元素
Status PushData(SqStack *S, SElemType e){
//栈已满
if (S->top == MAXSIZE -1) {
return ERROR;
}
//栈顶指针+1;
S->top ++;
//将新插入的元素赋值给栈顶空间
S->data[S->top] = e;
return OK;
}
1.3.3 顺序栈出栈
算法实现:
// 删除S栈顶元素,并且用e带回
Status Pop(SqStack *S,SElemType *e){
//空栈,则返回error;
if (S->top == -1) {
return ERROR;
}
//将要删除的栈顶元素赋值给e
*e = S->data[S->top];
//栈顶指针--;
S->top--;
return OK;
}
1.4 栈 - 链式栈实现
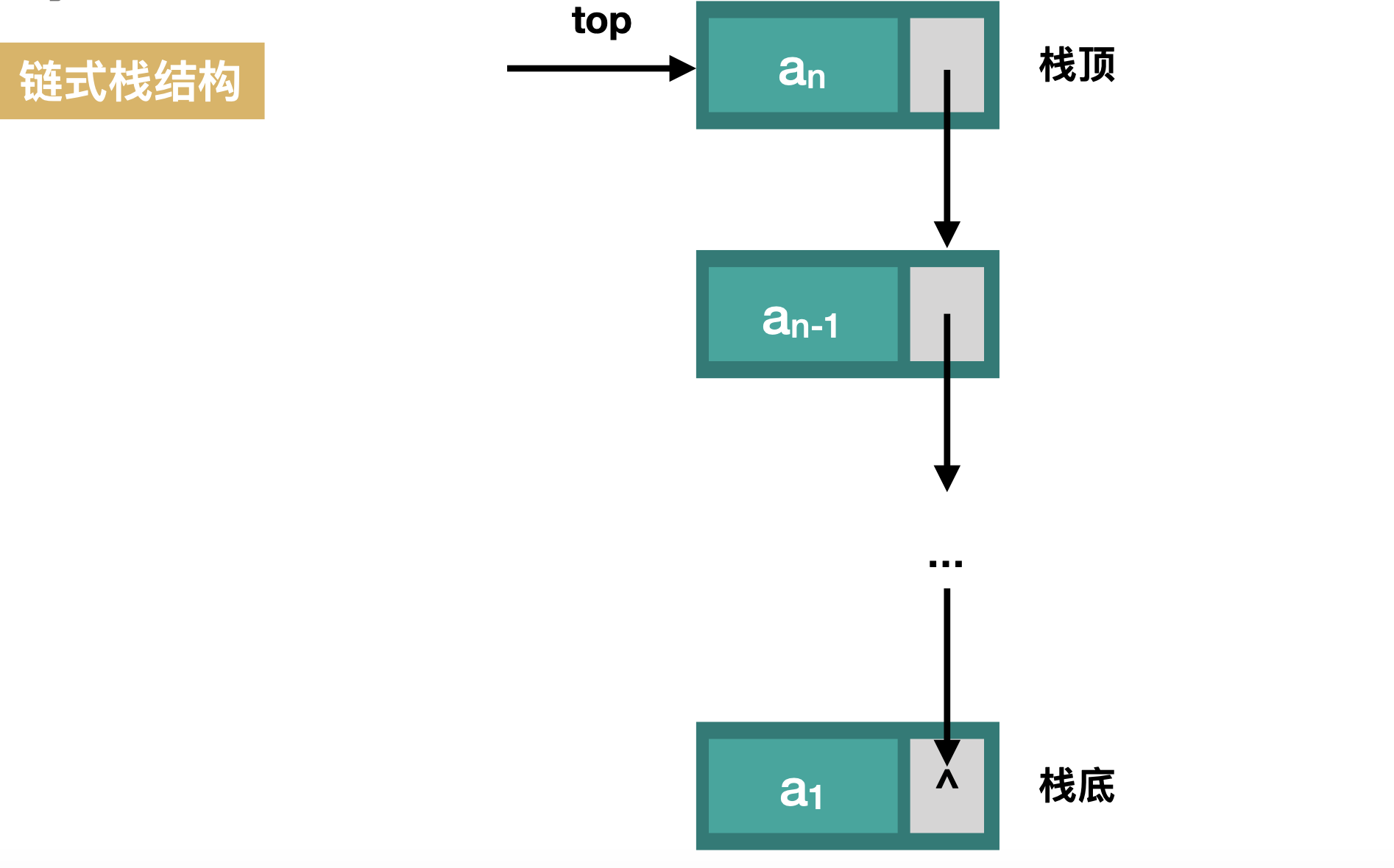
1.4.1 链式栈结构及初始化
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;
typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int */
/* 链栈结构 */
typedef struct StackNode
{
SElemType data;
struct StackNode *next;
}StackNode,*LinkStackPtr;
typedef struct
{
LinkStackPtr top;
int count;
}LinkStack;
/*5.1 构造一个空栈S */
Status InitStack(LinkStack *S)
{
S->top=NULL;
S->count=0;
return OK;
}
1.4.2 链式栈入栈
算法实现:
/*插入元素e到链栈S (成为栈顶新元素)*/
Status Push(LinkStack *S, SElemType e){
//创建新结点temp
LinkStackPtr temp = (LinkStackPtr)malloc(sizeof(StackNode));
//赋值
temp->data = e;
//把当前的栈顶元素赋值给新结点的直接后继, 参考图例第①步骤;
temp->next = S->top;
//将新结点temp 赋值给栈顶指针,参考图例第②步骤;
S->top = temp;
S->count++;
return OK;
}
1.4.3 链式栈出栈
算法实现:
/*若栈不为空,则删除S的栈顶元素,用e返回其值. 并返回OK,否则返回ERROR*/
Status Pop(LinkStack *S,SElemType *e){
LinkStackPtr p;
if (StackEmpty(*S)) {
return ERROR;
}
//将栈顶元素赋值给*e
*e = S->top->data;
//将栈顶结点赋值给p,参考图例①
p = S->top;
//使得栈顶指针下移一位, 指向后一结点. 参考图例②
S->top= S->top->next;
//释放p
free(p);
//个数--
S->count--;
return OK;
}
二、递归
什么是递归?若在一个函数的过程或数据结构定义的内部有直接(或间接)出现调用本身的应用;则称为他们是递归的,或者是递归定义。
下⾯面3种情况下,我们会使⽤用到递归来解决问题
2.1 定义是递归的
比如很多数学定义本身就是递归定义;例如阶乘
1、Fact(n)
(1) n=0, 1;
(2) n > 1, n*Fact(n-1);
2、二阶斐波拉契数列
Fib(n)
(1) n=1 n=2, 1;
(2) n > 2, Fib(n-1) + Fib(n-2);
经典的斐波拉契数列采用递归实现
int Fbi(int i){
if(i<2)
return i == 0?0:1;
return Fbi(i-1)+Fbi(i-2);
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("斐波拉契数列!\n");
// 1 1 2 3 5 8 13 21 34 55 89 144
for (int i =0; i < 10; i++) {
printf("%d ",Fbi(i));
}
printf("\n");
return 0;
}
对于类似复杂问题,若能够分解成几个简单且解法相同或类似的子问题来求解,便称为递归求解。
例如,在求解4时!先求解3!然后在进一步分解进行求解,这种求解方式叫做“分治法”。
采用“分治法”进行递归求解的问题需满足以下三个条件
- 能将一个问题转换变成一个小问题,而新问题和原问题解法相同或类同。不同的仅仅是处理的对象,并且这些处理更小且变化有规律的。
- 可以通过上述转换而使得问题简化
- 必须有一个明确的递归出口,或称为递归边界
2.2 数据结构是递归的
其数据结构本身具有递归的特性。
例如:对于链表,其结点Node的定义有数据域data和指针域next组成,而指针域nest是一种指向Node类型的指针,及Node的定义中又用到了其自身,所以链表是一种递归的数据结构。
// 链表结点
typedef struct Node{
ElemType data;
struct Node *next;
}Node;
2.3 问题的解法是递归的
有一类问题,虽然问题本身并没有明显的递归结构,但是采用递归求解比迭代求解更简单,如Hanoi问题、八皇后问题、迷宫问题。
Hanoi问题
#include <stdio.h>
int m = 0;
void moves(char X,int n,char Y){
m++;
printf("%d: from %c ——> %c \n",n,X,Y);
}
//n为当前盘子编号. ABC为塔盘
void Hanoi(int n ,char A,char B,char C){
//目标: 将塔盘A上的圆盘按规则移动到塔盘C上,B作为辅助塔盘;
//将编号为1的圆盘从A移动到C上
if(n==1) moves(A, 1, C);
else
{
//将塔盘A上的编号为1至n-1的圆盘移动到塔盘B上,C作为辅助塔;
Hanoi(n-1, A, C, B);
//将编号为n的圆盘从A移动到C上;
moves(A, n, C);
//将塔盘B上的编号为1至n-1的圆盘移动到塔盘C上,A作为辅助塔;
Hanoi(n-1, B, A, C);
}
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hanoi 塔问题\n");
Hanoi(3, 'A', 'B', 'C');
printf("盘子数量为3:一共实现搬到次数:%d\n",m);
Hanoi(4, 'A', 'B', 'C');
printf("盘子数量为3:一共实现搬到次数:%d\n",m);
return 0;
}
三、递归过程与递归工作栈
一个递归函数,在函数执行过程中,需要多次进行自我调用,在高级语言程序中,调用函数和被调用函数之间的链接与信息交换都是通过栈来进行。
通常,当一个函数在运行期间调用另一个函数时,在运行被调用函数之前,系统需要完成3件事情:
- 将所有的实参,返回地址等信息调用传递到被调用函数保存;
- 为被调用函数的局部变量分配存储空间;
- 将控制移动到被调函数入口;
而从被调用函数返回调用函数之前,系统同样需要完成3件事:
- 保存被调用函数的计算结果;
- 释放被调用函数的数据区;
- 依照被调用函数保存的返回地址将控制移动到调用函数;
当多个函数构成嵌套调用时,按照“先调用后返回”的原则,上述函数之间的信息传递和控制转移必须通过“栈”来实现。即系统将整个程序运行时的所需要的数据空间都安排在一个栈中,每当调用一个函数时,就在它的栈顶分配一个存储区。每当这个函数退出时,就释放它的存储区。则当前运行是的函数的数据区必在栈顶。
看下面一个函数的运行:

上面主函数main中调用了函数first,而在函数first又嵌套调用了second函数,则当我们执行first时栈空间里保存了a图如下信息,当我们执行second时保存了b图如下信息。
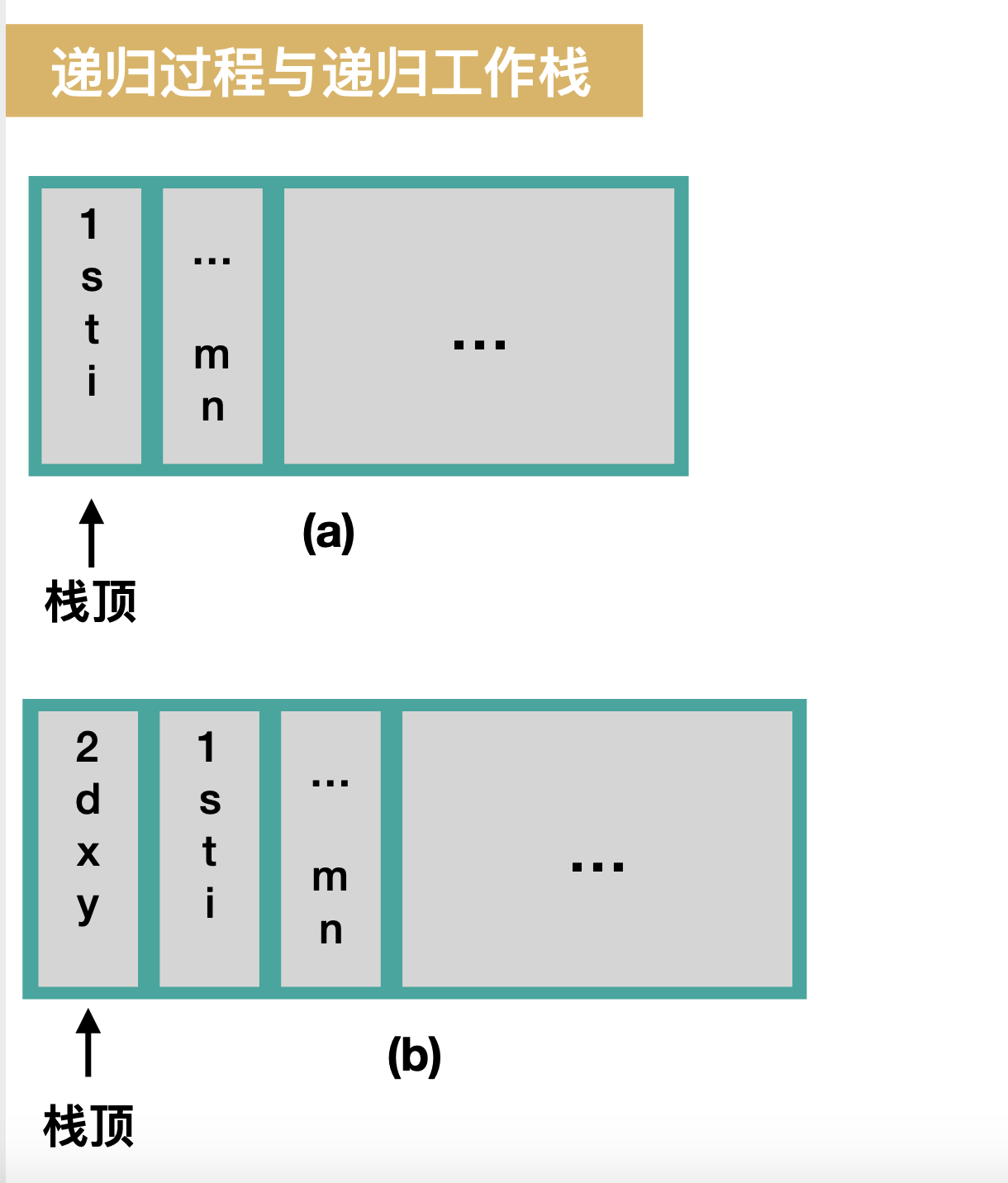
一个递归函数的运行过程中就是类似上面的多层函数嵌套,这就是递归函数运行的“层次”,为了保证递归函数的正确执行,系统就要建立一层一层的的工作栈,每层工作栈保留了所有的实参,局部变量,以及上一层的返回地址,形成工作记录压入栈顶,就形成了递归工作栈。