# 从零开始的数据结构与算法（七）：队列

1 定义

队列和栈一样是一种重要的数据结构。不同于栈“先进后出”的规则，它正如其名，是一种“先进先出(FIFO-First In First Out)”的结构。

在生活中，我们买东西排队就是典型的队列结构：先入队的人先买先出列，后入队的人需等待前面的数据元素出队。

在开发中，执行多任务、创建数据缓冲区等都是队列结构的应用。下面将介绍队列的具体实现。

2 顺序存储队列

首先，使用顺序存储的方式创建一块连续的内存，以数组的形式保存队列中的数据元素。

新元素入队则添加在数组中原有元素的后面。出队时则将首个元素移除，并需要将所有元素向前移动一格，这种数据移动会产生不必要的计算。所以采用如下的管理方式。

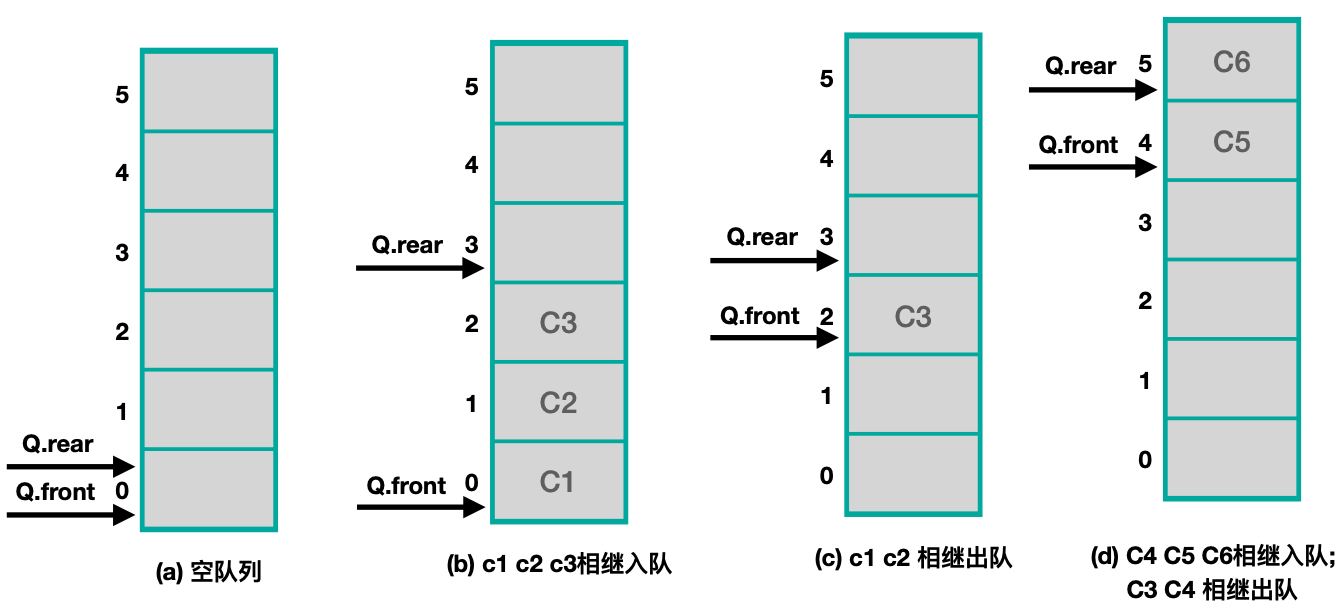
使用两个下标 rear front来标记队列的对头和队尾。入队时在rear 出插入数据，出队时在 front 出移除数据。这样就避免了不必要的数据移动操作。

如果队尾 rear 移动到了空间的最后一格，此时如果有新的元素入队，因为空间是固定的不能开辟新的空间，并且之前的空间已被释放，如果不用则会造成浪费，所以在此基础上提出了循环队列的概念。

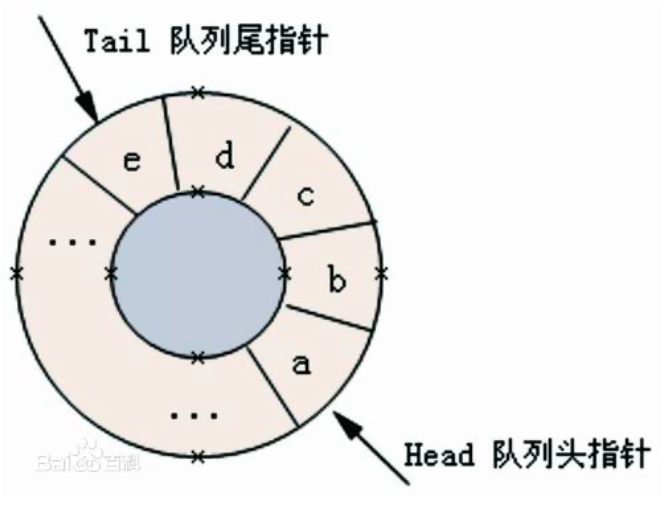
当队尾 rear 移动到最后的一格入队时，会让队尾 rear 重新回到空间的起始位置，将新的数据元素插入到前面已被释放的空间中，使空间循环地利用。队列通过两个队标来判断当前的状态，循环可以通过取模运算 % 来实现。

在数据元素为空时， 队头front 与队尾 rear 都指向空间的起始地址。当数据元素存满时，队头front 与队尾 rear 又指向同样的地址，此时将无法判断队列是空的还是满的。为解决这个问题，我们将牺牲一个存储单元作为标记，规定队头front 在队尾 rear 前面距离一个存储单元时队列为满的状态，如下图所示：

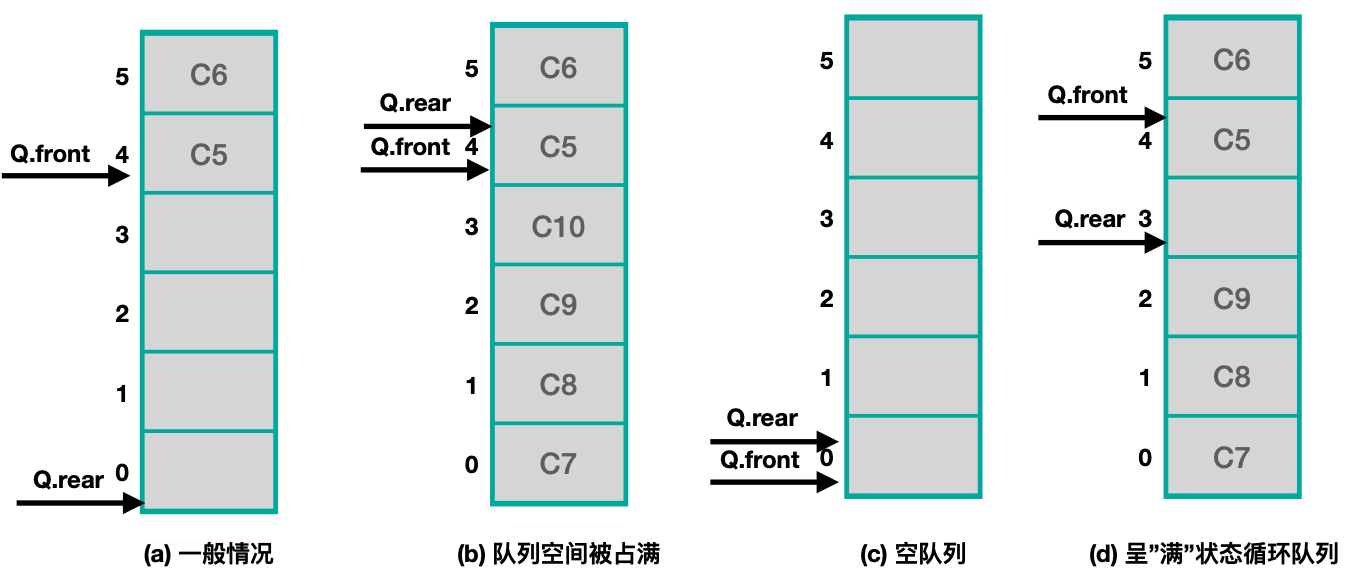
图 c 表示队列开始的状态。当元素不断地入队后成为图 d 时，则认为当前队列已满，以区分队列为空的状态。

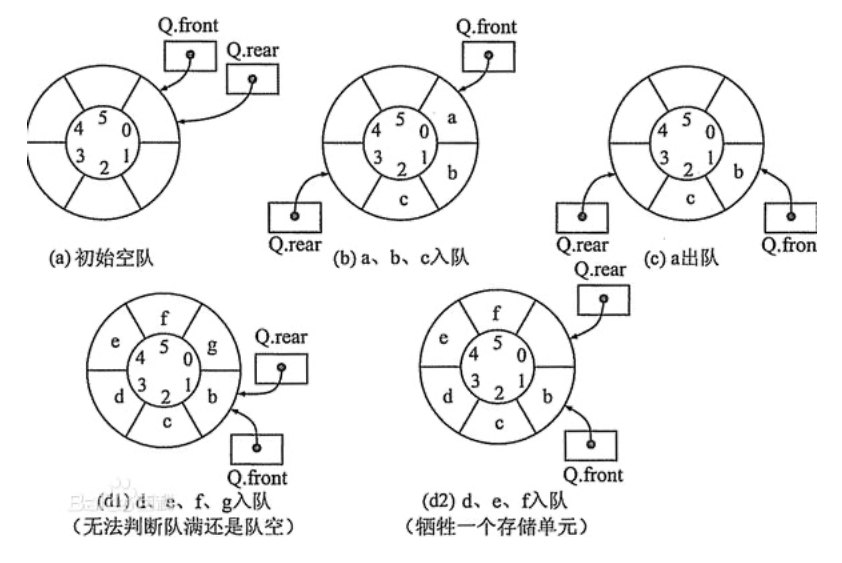
下图展示了将物理内存“掰弯”后，队列结构的操作顺序：

2.1 结构定义

/// 设置队列的长度
#define MAXSIZE 10
/// 顺序存储队列结构
typedef struct {
    ElementType data[MAXSIZE];  // 连续内存空间
    int front;  // 对头下标，指向对头元素
    int rear;   // 队尾下标，指向队尾元素的下一个位置
} Queue;

2.2 队列常用方法

/// 初始化顺序存储队列
static Status queueInit(Queue *q) {
    q->front = 0;
    q->rear = 0;
    return SUCCESS;
}

/// 清空顺序存储队列
static Status queueClear(Queue *q) {
    // 数据不需要抹除，只需改变下标位置
    q->front = 0;
    q->rear = 0;
    return SUCCESS;
}

/// 判断队列是否为空
static int queueIsEmpty(Queue q) {
    if (q.front == q.rear) {
        return 1;
    }
    return 0;
}

/// 判断队列是否已满
static int queueIsFull(Queue q) {
    if ((q.rear + 1) % MAXSIZE == q.front) {
        return 1;
    }
    return 0;
}

/// 获取队列的长度
static int queueLength(Queue q) {
    return (q.rear - q.front + MAXSIZE) & MAXSIZE;
}

/// 获取队头元素
static Status getHeadElement(Queue q, ElementType *e) {
    // 空队列判断
    if (q.front == q.rear) {
        return ERROR;
    }
    // 队头元素
    *e = q.data[q.front];
    return SUCCESS;
}

/// 遍历打印队列的数据元素
static Status queueTraverse(Queue q) {
    int i = q.front;
    printf("[队头-队尾]Queue: ");
    while (i != q.rear) {
        printf("%d ", q.data[i]);
        i = (i + 1) % MAXSIZE;
    }
    printf("\n");
    return SUCCESS;
}

2.3 入队

/// 数据元素入队
static Status enqueue(Queue *q, ElementType e) {
    // 队列已满判断
    if ((q->rear + 1) % MAXSIZE == q->front) {
        return ERROR;
    }
    // 队尾设置新的数据
    q->data[q->rear] = e;
    // 改变队尾位置，加一取模
    q->rear = (q->rear + 1) % MAXSIZE;
    return SUCCESS;
}

2.4 出队

/// 数据元素出队
static Status dequeue(Queue *q, ElementType *e) {
    // 空队列判断
    if (q->front == q->rear) {
        return ERROR;
    }
    // 返回数据元素的数据
    *e = q->data[q->front];
    // 改变队头位置
    q->front = (q->front + 1) % MAXSIZE;
    return SUCCESS;
}

2.5 使用

int main() {
    Queue q;
    printf("队列初始化\n");
    queueInit(&q);
    queueTraverse(q);
    printf(queueIsEmpty(q) ? "\n队列是空的\n" : "\n队列不为空\n");
    
    printf("\n构建队列\n");
    for (int i = 0; i < 10; i++) {
        ElementType element = i * 4 + 1;
        enqueue(&q, element);
    }
    printf(queueIsFull(q) ? "\n队列是满的\n" : "\n队列没有满\n");
    queueTraverse(q);
    printf("队列的元素个数为 %d\n", queueLength(q));
    ElementType head;
    getHeadElement(q, &head);
    printf("队头的元素数据为 %d\n", head);

    ElementType e = 666;
    printf("\n入队 ← %d\n", e);
    enqueue(&q, e);
    queueTraverse(q);

    ElementType e1;
    dequeue(&q, &e1);
    printf("\n出队 → %d\n", e1);
    queueTraverse(q);
    
    ElementType e2;
    dequeue(&q, &e2);
    printf("\n出队 → %d\n", e2);
    queueTraverse(q);

    printf("\n清空队列 x\n");
    queueClear(&q);
    queueTraverse(q);
    return 0;
}

打印结果：

队列初始化
[队头-队尾]Queue: 

队列是空的

构建队列

队列是满的
[队头-队尾]Queue: 1 5 9 13 17 21 25 29 33 
队列的元素个数为 2
队头的元素数据为 1

入队 ← 666
[队头-队尾]Queue: 1 5 9 13 17 21 25 29 33 

出队 → 1
[队头-队尾]Queue: 5 9 13 17 21 25 29 33 

出队 → 5
[队头-队尾]Queue: 9 13 17 21 25 29 33 

清空队列 x
[队头-队尾]Queue: 

3 链式存储队列

链式存储由于不受起始空间的限制，所以不存在顺序存储队列所存在的位置计算问题，在实现上要比顺序存储简单一些。

3.1 结构定义

/*
/// 设置队列的长度
#define MAXSIZE 10
/// 顺序存储队列结构
typedef struct {
    ElementType data[MAXSIZE];  // 连续内存空间
    int front;  // 对头下标，指向对头元素
    int rear;   // 队尾下标，指向队尾元素的下一个位置
} Queue;
*/

/// 队节点结构
/// next 指向下一个要出队的元素
typedef struct QueueNode {
    ElementType data;           // 数据域
    struct QueueNode *next;     // 后继指针
} *QueueNodePtr;

/// 队列结构创建
typedef struct {
    QueueNodePtr front; // 队头位置
    QueueNodePtr rear;  // 队尾位置
} LinkQueue;

3.1 初始化

/// 初始化顺序存储队列
static Status queueInit(LinkQueue *q) {
    // 创建头结点作为辅助节点
    QueueNodePtr head = (QueueNodePtr)malloc(sizeof(struct QueueNode));
    if (!head) {
        return ERROR;
    }
    head->next = NULL;
    // 队头队尾指向新的节点
    q->front = q->rear = head;
    return SUCCESS;
}

在初始化中，创建了一个头结点作为链表的辅助节点，和前几节中链表的头结点作用一样，为了避免首节点的判断操作。此时，front->next 才是链表的首元节点，也就是队头元素。当队列为空时，队头 front 队尾 rear 都指向这个头结点。

3.2 清空

/// 清空顺序存储队列
static Status queueClear(LinkQueue *q) {
    // 获取队头元素
    QueueNodePtr p = q->front->next;
    QueueNodePtr temp;
    // 遍历释放各节点
    while (p) {
        temp = p;
        free(temp);
        p = p->next;
    }
    // 重置队头与队尾
    q->front->next = NULL;
    q->rear = q->front;
    return SUCCESS;
}

/// 销毁顺序存储队列
static Status queueDestroy(LinkQueue *q) {
    // 释放所有节点和头结点
    while (q->front) {
        // 利用 q->rear 作为 temp
        q->rear = q->front->next;
        free(q->front);
        q->front = q->rear;
    }
    // 注意 while 中的顺序，保证 rear 和 front 都为 NULL
    return SUCCESS;
}

3.3 队列常用方法

/// 判断队列是否为空
static int queueIsEmpty(LinkQueue q) {
    if (q.front == q.rear) {
        return 1;
    }
    return 0;
}

/// 获取队列的长度
static int queueLength(LinkQueue q) {
    int len = 0;
    QueueNodePtr p = q.front;
    // 队头到队尾遍历计算长度
    while (p != q.rear) {
        p = p->next;
        len++;
    }
    return len;
}

/// 获取队头元素
static Status getHeadElement(LinkQueue q, ElementType *e) {
    // 空队列判断
    if (q.front == q.rear) {
        return ERROR;
    }
    // 队头元素()
    *e = q.front->next->data;
    return SUCCESS;
}

/// 遍历打印队列的数据元素
static Status queueTraverse(LinkQueue q) {
    QueueNodePtr p = q.front->next;
    printf("[队头-队尾]Queue: ");
    while (p) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
    return SUCCESS;
}

3.4 入队

/// 数据元素入队
static Status enqueue(LinkQueue *q, ElementType e) {
    QueueNodePtr temp = (QueueNodePtr)malloc(sizeof(struct QueueNode));
    if (!temp) {
        return ERROR;
    }
    temp->data = e;
    temp->next = NULL;
    // 添加到队尾，即链表后面
    q->rear->next = temp;
    // 移动队尾位置
    q->rear = temp;
    return SUCCESS;
}

3.5 出队

/// 数据元素出队
static Status dequeue(LinkQueue *q, ElementType *e) {
    // 空队列判断
    if (q->front == q->rear) {
        return ERROR;
    }
    // 出队列的节点
    QueueNodePtr temp = q->front->next;
    // 改变队头位置
    q->front->next = temp->next;
    // 队头也是队尾，即只有一个元素，则重置队尾
    if (temp == q->rear) {
        q->rear = q->front;
    }
    // 返回数据元素的数据
    *e = temp->data;
    // 释放节点
    free(temp);
    return SUCCESS;
}

3.6 使用

int main() {
    LinkQueue q;
    printf("队列初始化\n");
    queueInit(&q);
    queueTraverse(q);
    if (queueIsEmpty(q)) {
        printf("\n队列是空的\n");
    } else {
        printf("\n队列不为空\n");
    }
    
    printf("\n构建队列\n");
    for (int i = 0; i < 6; i++) {
        ElementType element = i * 2 + 3;
        enqueue(&q, element);
    }
    queueTraverse(q);
    printf("队列的元素个数为 %d\n", queueLength(q));
    ElementType head;
    getHeadElement(q, &head);
    printf("队头的元素数据为 %d\n", head);

    ElementType e = 777;
    printf("\n入队 ← %d\n", e);
    enqueue(&q, e);
    queueTraverse(q);

    ElementType e1;
    dequeue(&q, &e1);
    printf("\n出队 → %d\n", e1);
    queueTraverse(q);
    
    ElementType e2;
    dequeue(&q, &e2);
    printf("\n出队 → %d\n", e2);
    queueTraverse(q);

    printf("\n清空队列 x\n");
    queueClear(&q);
    queueTraverse(q);
    return 0;
}

打印结果：

队列初始化
[队头-队尾]Queue: 

队列是空的

构建队列
[队头-队尾]Queue: 3 5 7 9 11 13 
队列的元素个数为 6
队头的元素数据为 3

入队 ← 777
[队头-队尾]Queue: 3 5 7 9 11 13 777 

出队 → 3
[队头-队尾]Queue: 5 7 9 11 13 777 

出队 → 5
[队头-队尾]Queue: 7 9 11 13 777 

清空队列 x
[队头-队尾]Queue: