二叉树的顺序存储和链式存储

Potato_土豆
471 阅读6分钟

  • 树结构图解

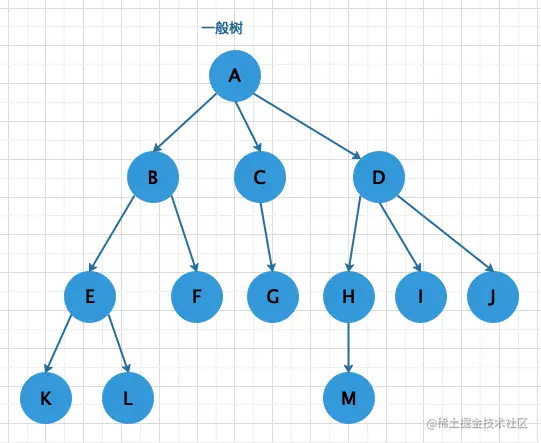
  • 树的一些概念

    1. 结点： 树中的⼀个独⽴单元. 包含⼀个数据元素及若⼲指向其他⼦树的分⽀. 例如, A,B,C,D等都是结点;
    2. 结点的度：结点拥有的子树的个数，A的度是3，B的度是2；
    3. 树的度：所有结点中的度的最大值就是树的度，上图树的度是3；
    4. 非终端结点：度不为0的结点
    5. 双亲和孩子：结点的子树称之为该节点的孩子。对应的该结点是孩子的双亲
    6. 兄弟：双亲相同的结点；
    7. 祖先：从根到该结点经历的所有结点；
    8. 子孙：以某结点为根的⼦树中的任⼀结点都称为该结点的⼦树. 例如,B的⼦孙为E,F；
    9. 层次：结点的层次从根开始定义起, 根为第⼀层, 根的孩⼦为第⼆层. 树中任⼀层次等于双亲结点的层次 加1；
    10. 堂兄弟：双亲在同一层，并且互相双亲不是同一个结点；
    11. 有序树和无序树：如果将树的结点的各⼦树看成从左到右是有次序的(即不能互换)则称为该树为有序树, 否则是⽆序树，在有序树中最左边的⼦树的根称为第⼀个孩⼦,最右边的称为最后⼀个孩⼦；
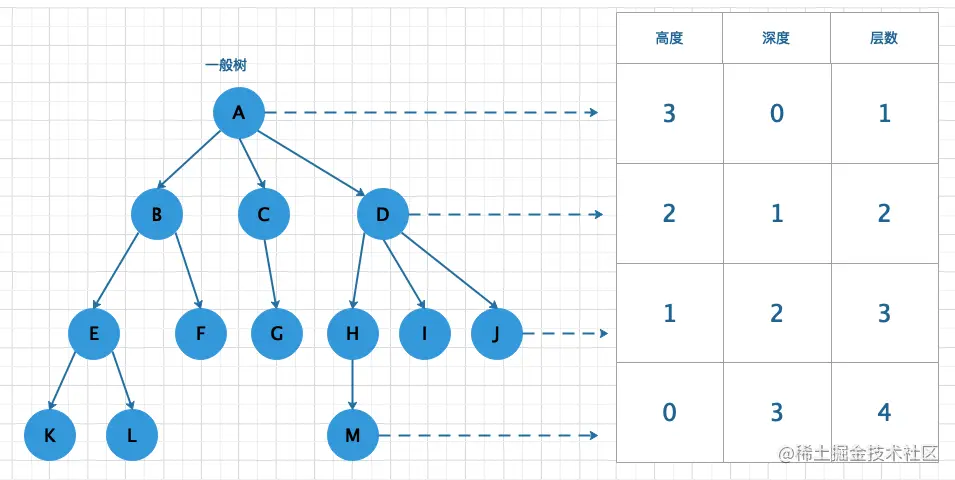
    12. 结点的高度：结点到叶子结点的最长路径；
    13. 结点的深度：根结点到该结点经历的边数；
    14. 结点的层数：结点的深度+1
    15. 树的高度：根节点到叶子结点的最长路径

  • 树结构中的高度、深度以及层数图解

  • 二叉树图解

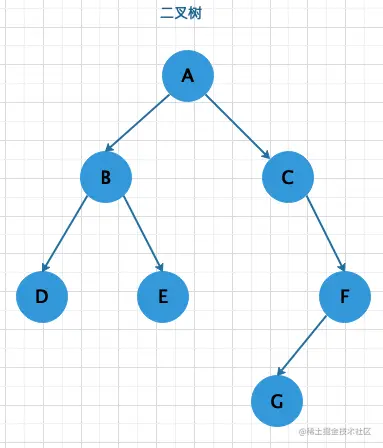
  • 二叉树概念

    • 二叉树的特性

      1. ⼆叉树每个结点⾄多只有2颗⼦树(⼆叉树中不存在度⼤于2的结点). 所以⼆叉树中不存在⼤于2的结点. 注意: 不是只有2个⼦树,⽽是最多只有. 如果⼆叉树中没有⼦树或者只有⼀颗树是可以的
      2. ⼆叉树的⼦树有左右之分,其次序不能任意颠倒
      3. 即使只有⼀棵树,也需要区分是左⼦树还是右⼦树

    • 二叉树的性质

      1. 在二叉树的第i层上最多有2^(i-1)个结点
      2. 深度为K的二叉树最多有2k -1 个结点(K>=1)
      3. 对于任何一颗二叉树T,如果其终端结点数为n0,度为2的结 点数为n2,则n0 = n2 + 1
      4. 具有n个结点的完全二叉树深度为(log2(n))+1
      5. 对具有n个结点的完全二叉树，如果按照从上至下和从左至右的顺序对二 叉树的所有结点从1开始编号，则对于任意的序号为i的结点有:
        A.如果i>1，那么序号为i的结点的双亲结点序号为i/2；
        B.如果i=1，那么序号为i的结点为根节点，无双亲结点；
        C.如果2i<=n，那么序号为i的结点的左孩子结点序号为2i；
        D.如果2i>n，那么序号为i的结点无左孩子；
        E.如果2i+1<=n，那么序号为i的结点右孩子序号为2i+1；
        F.如果2i+1>n，那么序号为i的结点无右孩子。

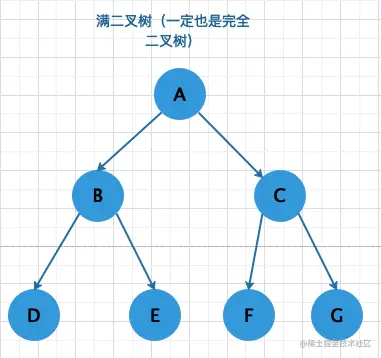
    • 满二叉树

      所有非终端结点的度都等于2

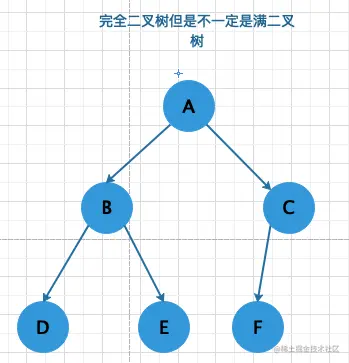
    • 完全二叉树

      对⼀颗具有n个结点的⼆叉树按层序编号,如果编号为i(1=< i <= n)的结点与同样深度的满⼆叉树中编号为i 的结点⼆叉树中位置完全相同. 则这颗⼆叉树称为完全⼆叉树.

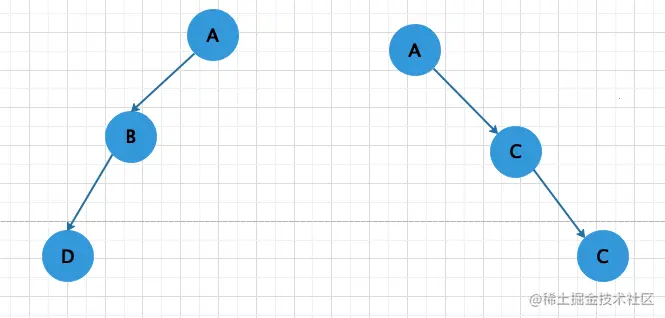
    • 斜树

      只有左子树或者右子树的二叉树

  • 二叉树的遍历

    • 层序遍历

      按照树的层依次冲左向右遍历,例如上图的满二叉树的遍历结果是A、B、C、D、E、F、G

    • 先序遍历

      先打印根结点然后是先序遍历左子树，然后先序遍历右子树（主要是先打印根然后按照左右打印）例如上图的满二叉树的遍历结果是：A、B、D、E、C、F、G

    • 中序遍历

      通俗的话说找到坐子树的叶子结点，然后找到其双亲按照左孩子双亲右孩子的次序打印，然后打印根节点然后左子树也找上上述规则打印（右根左的次序），例如上图的满二叉树的遍历结果是D、E、B、A、F、C、G

    • 后序遍历

      一样从左子树开始找到叶子结点依次打印然后打印双亲，依次往上直到双亲为根节点，然后右子树一样按照上述规则遍历，最后打印根节点，例如上图的满二叉树的遍历结果是D、E、B、F、G、C、A

  • 二叉树的顺序存储实现

    按照层依次从左到右存储，如果碰见当前结点是空节点，但是后续还有结点的情况则当前结点置为空（存储的结构应该按照完全二叉树的结构存储，如没有结点则补上空节点），例如上图中的二叉树的图，顺序存储后的树结构应该是下图 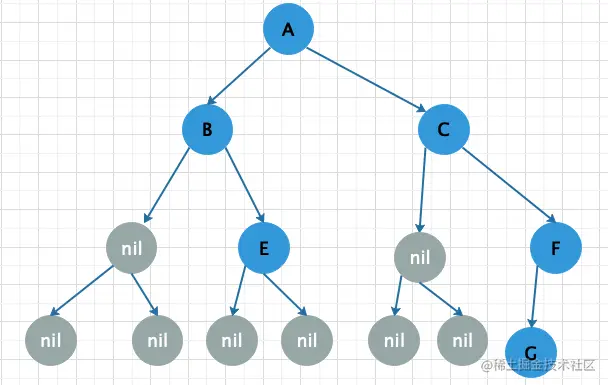注：顺序存储只适合完全二叉树，其他二叉树会浪费空间
#include <stdio.h>
#include "stdlib.h"

#include "math.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAX_TREE_SIZE 100 /* 二叉树的最大结点数 */

typedef int Status;
typedef int ElemType;  //树结点的类型，也可以是字符型



typedef struct {
    int level;   //层数
    int order;   //结点在当前层的序号
}Position;

typedef ElemType Tree[MAX_TREE_SIZE];
ElemType Nil = 0;  //这里设置-1说明是空节点，

//初始化
Status initTree(Tree T){
    for(int i = 0; i < MAX_TREE_SIZE; i ++){
        T[i] = Nil;
    }
    return OK;
}

//创建树（向树里面插入值，完全二叉树）
Status createTree(Tree T){
    for(int i = 1; i <= 10; i ++){
        T[i-1] = i;
        //如果没有双亲并且当前结点还不是Nil则抛出异常
        if(i != 0 && T[(i+1)/2-1] == Nil && T[i] == Nil){
            printf("二叉树异常");
            exit(0);
        }
    }
    return OK;
}

Status TreeEmpty(Tree T){
    //只需要判断根节点是否为nil
    if(T[0] == Nil) return TRUE;
    return FALSE;
}

//树的深度
int TreeDepth(Tree T){
    if(TreeEmpty(T)) return ERROR;
    //先求出最后一个结点的序号
    int i = MAX_TREE_SIZE - 1;
    for(; T[i] == Nil; i --);
    
    int j = 0;
    while ((i + 1)/2 -1 >= 0) {
        j ++;
        i = (i + 1)/2 -1;
    }
    return j;
}

//返回某个位置的结点
ElemType value(Tree T, Position p){
    //先求出对应位置的下标
    int index = pow(2, p.level - 1) - 1 + p.order - 1;
    return T[index];
}

//获取根节点
ElemType Root(Tree T){
    return T[0];
}

//给e位置的结点赋值
Status setValue(Tree T,Position p,ElemType e){
    if(TreeEmpty(T)) return ERROR;
    int index = pow(2, p.level - 1) - 1 + p.order - 1;
    //如果双亲为空则报错
    if(T[(index +1)/2 - 1] == Nil) return ERROR;
    //如果将要赋值的值为nil，但是当前结点含有孩子结点，则报错
    if(e == Nil && (T[index *2 + 1] != Nil))
    T[index] = e;
    return OK;
}

//获取值为e的双亲
ElemType getParent(Tree T, ElemType e){
    int i = 0;
    for(;i < MAX_TREE_SIZE; i ++){
        if(T[i] == e) break;
    }
    if(i > 0){
        if(T[(i + 1)/2 - 1] == Nil) return ERROR;
        return T[(i + 1)/2 - 1];
    }
    return Nil;
}

/* 获取某个结点的左孩子;
初始条件:二叉树T存在,e是某个结点
操作结果:返回e的左孩子,若e无左孩子,则返回"空"
*/
ElemType getLeftChild(Tree T, ElemType e){
    if(TreeEmpty(T)) return ERROR;
    int i = 0;
    for(;i < MAX_TREE_SIZE; i ++){
        if(T[i] == e) {
            return T[2*i +1];
        }
    }
    return Nil;
}

/* 获取某个结点的右孩子;
初始条件:二叉树T存在,e是某个结点
操作结果:返回e的左孩子,若e无左孩子,则返回"空"
*/
ElemType getRightChild(Tree T, ElemType e){
    if(TreeEmpty(T)) return ERROR;
    int i = 0;
    for(;i < MAX_TREE_SIZE; i ++){
        if(T[i] == e) {
            return T[2*i +2];
        }
    }
    return Nil;
}

/* 获取结点的左兄弟
初始条件:  二叉树T存在,e是T中某个结点
操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回＂空＂
*/
ElemType getLeftBrothers(Tree T, ElemType e){
    if(TreeEmpty(T)) return ERROR;
    int i = 1;
    for(;i < MAX_TREE_SIZE; i ++){
        if(T[i] == e) {
            //说明当前结点就是T的做孩子
            if(i%2 != 0) return Nil;
            else if(T[i-1] == Nil) return Nil;
            return T[i-1];
        }
    }
    return Nil;
}

/* 获取结点的右兄弟
初始条件: 二叉树T存在,e是T中某个结点
操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回＂空＂
*/
ElemType getRightBrothers(Tree T, ElemType e){
    if(TreeEmpty(T)) return ERROR;
    int i = 1;
    for(;i < MAX_TREE_SIZE; i ++){
        if(T[i] == e) {
            //说明当前结点就是T的右孩子
            if(i%2 == 0) return Nil;
            else if(i+1 >= MAX_TREE_SIZE) return Nil;
            return T[i+1];
        }
    }
    return Nil;
}

#pragma mark -- 二叉树的遍历

/*
 层序遍历二叉树
*/
void LevelOrderTraverse(Tree T){
    if(TreeEmpty(T)) return;
    //先求出树的最后一个元素的序号
    int index = MAX_TREE_SIZE -1;
    for(;T[index] == Nil; index --);
    
    for(int i = 0; i <= index; i ++){
        printf("%d ",T[i]);
    }
}

/*
 前序遍历二叉树
 e指定位置开始遍历
 */
void PreTraverse(Tree T,int e){
    if(TreeEmpty(T)) return;
    //先打印根节点
    printf("%d ",T[e]);
    
    //在遍历左子树
    if(T[e*2 +1] != Nil)
        PreTraverse(T, e*2 +1);
    //然后遍历右子树
    if(T[2*e +2] != Nil)
        PreTraverse(T, 2*e +2);
}

/*
中序遍历二叉树
e指定位置开始遍历
*/
void InTraverse(Tree T, int e){
    if(TreeEmpty(T)) return;
    //先遍历左子树
    if(T[e*2 +1] != Nil)
        InTraverse(T, e*2 +1);
    
    //打印节点
    printf("%d ",T[e]);
    
    //然后遍历右子树
    if(T[2*e +2] != Nil)
        InTraverse(T, 2*e +2);
}

/*
后序遍历二叉树
e指定位置开始遍历
*/
void PostTraverse(Tree T,int e){
    if(TreeEmpty(T)) return;
    //先遍历左子树
    if(T[e*2 +1] != Nil)
        PostTraverse(T, e*2 +1);
    
    //然后遍历右子树
    if(T[2*e +2] != Nil)
        PostTraverse(T, 2*e +2);
    
    //最后打印节点
    printf("%d ",T[e]);
}

int main(int argc, const char * argv[]) {
    // insert code here...
    Tree T;
    initTree(T);
    createTree(T);
    printf("层序遍历的结果：");
    LevelOrderTraverse(T);
    printf("\n");
    printf("先序遍历的结果：");
    PreTraverse(T,0);
    printf("\n");
    printf("中序遍历的结果：");
    InTraverse(T,0);
    printf("\n");
    printf("后序遍历的结果：");
    PostTraverse(T,0);
    printf("\n");
    return 0;
}

  • 二叉树的链式存储实现

#include <stdio.h>
#include "string.h"
#include "stdlib.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define Nil ' '

typedef int Status;
typedef char ElemType;  //树结点的字符型，也可以是整型
int indexs = 0;

typedef struct TreeNode{
    ElemType data;  //数据
    struct TreeNode *lchild; //指向左孩子的指针
    struct TreeNode *rchild; //指向右孩子的指针
}TreeNode, *Tree;

char *TreeStr = "ABDH#K###E##CFI###G#J##";


//初始化
Status initTree(Tree *T){
    *T = NULL;
    return OK;
}

//销毁二叉树
Status DestroyTree(Tree *T){
    if(*T == NULL) return OK;
    if((*T)->lchild){
        DestroyTree(&(*T)->lchild);
    }
    if((*T)->rchild){
        DestroyTree(&(*T)->rchild);
    }
    
    free(*T);
    *T = NULL;
    
    return OK;
}

/* 创建二叉树
按前序输入二叉树中的结点值(字符),#表示空树;
ABDH#K###E##CFI###G#J##
*/
void CreateTree(Tree *T){
    ElemType data;
    if(indexs < (int)strlen(TreeStr)){
        data = TreeStr[indexs++];
        if(data != '#'){
            *T = (Tree)malloc(sizeof(TreeNode));
            if(*T == NULL) exit(0);
            (*T)->data = data;
            CreateTree(&((*T)->lchild));
            CreateTree(&((*T)->rchild));
        }else{
            *T = NULL;
        }
    }
    
}

/*
 二叉树T的深度
 初始条件: 二叉树T存在
 操作结果: 返回T的深度
 */
int TreeDepth(Tree T){
    if(T == NULL) return ERROR;
    int i,j;
    if(T->lchild){
        i = TreeDepth(T->lchild);
    }else{
        i = 0;
    }
    if(T->rchild){
        j = TreeDepth(T->rchild);
    }else{
        j = 0;
    }
    return i>j ? i+1:j+1;
}

/*
前序递归遍历T
 初始条件:二叉树T存在;
 操作结果: 前序递归遍历T
 */

void PreOrderTraverse(Tree T){
    if(T == NULL) return;
    
    printf("%c ",T->data);
    
    PreOrderTraverse(T->lchild);
    PreOrderTraverse(T->rchild);
    
}

/*
 中序递归遍历T
 初始条件:二叉树T存在;
 操作结果: 中序递归遍历T
 */
void InOrderTraverse(Tree T){
    if(T == NULL) return;
    InOrderTraverse(T->lchild);
    printf("%c ",T->data);
    InOrderTraverse(T->rchild);
}

/*
7.10  后序递归遍历T
初始条件:二叉树T存在;
操作结果: 中序递归遍历T
*/
void PostOrderTraverse(Tree T){
    if(T == NULL) return;
    PostOrderTraverse(T->lchild);
    PostOrderTraverse(T->rchild);
    printf("%c ",T->data);
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    Tree T;
    CreateTree(&T);
    printf("%d",TreeDepth(T));
    printf("\n");
    PreOrderTraverse(T);
    printf("\n");
    InOrderTraverse(T);
    printf("\n");
    PostOrderTraverse(T);
    return 0;
}
avatar
文章
阅读
粉丝