最短路径

最短路径问题是图的一个比较典型的应用问题。例如，某一地区的一个公路网，给定了该网内的n个城市及这些城市之间的相通公路的距离，能否找到城市A到城市B之间一条距离最近的通路呢？如果将城市用顶点表示，城市间的公路用边表示，公路的长度作为边的权值，那么，这个问题就可归结为在网中求点A到点B的所有路径中边的权值之和最短的那一条路径。这条路径就是两点之间的最短路径，并称路径上的第一个顶点为源点（Sourse），最后一个顶点为终点（Destination）。在不带权的图中，最短路径是指两点之间经历的边数最少的路径。 最短路径可以是求某个源点出发到其他顶点的最短路径，也可以是求图中任意两个顶点之间的最短路径。

Dijkstra(迪杰斯特拉)算法

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

算法描述

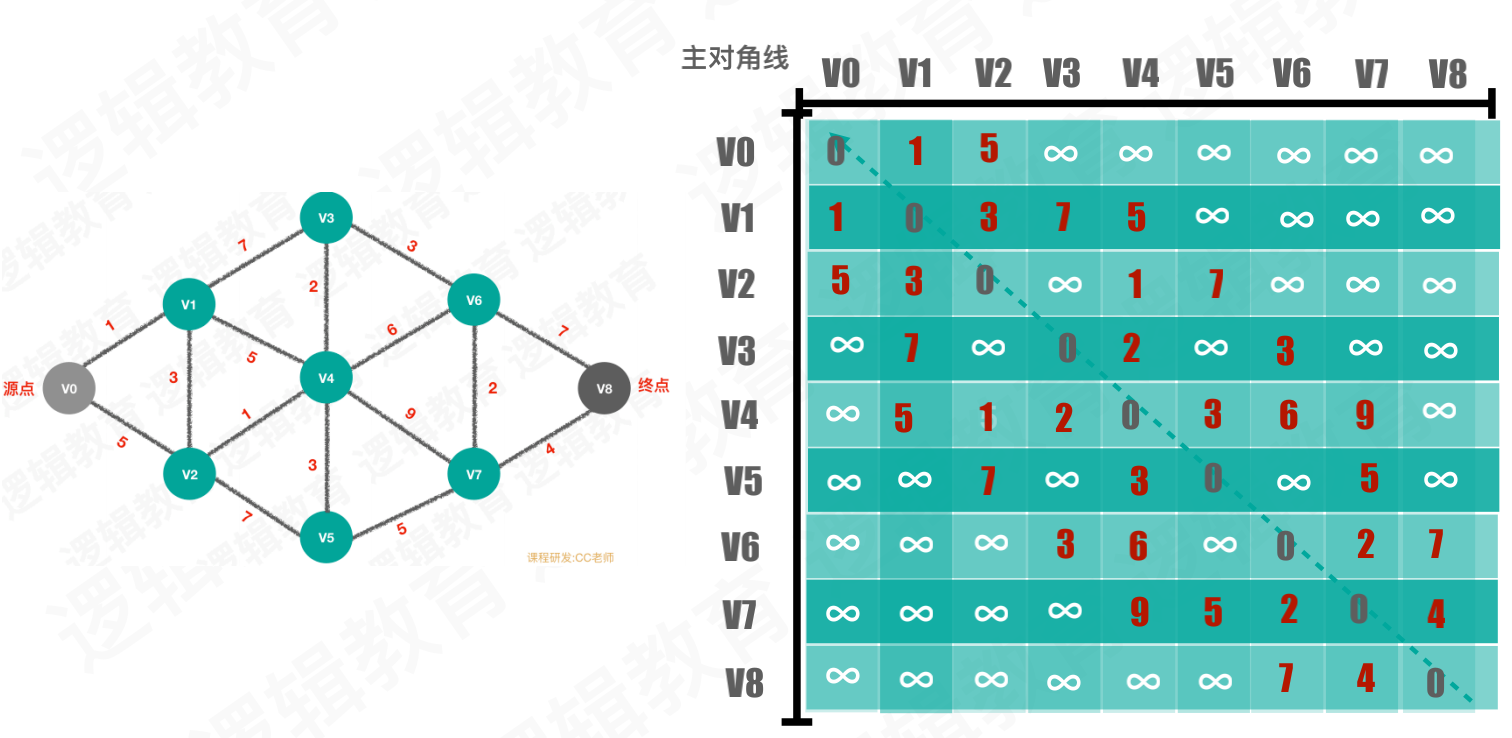
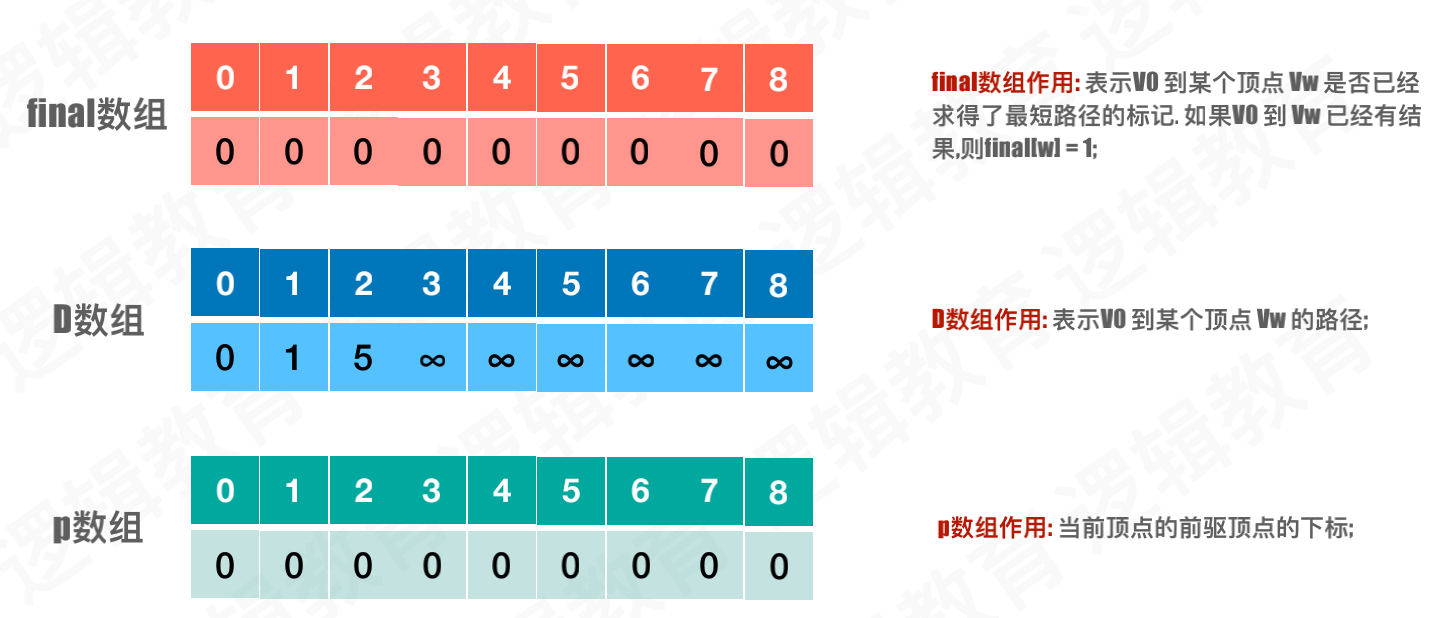
a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

代码实现

{
    int v,w,k,min;
    k = 0;
    /*final[w] = 1 表示求得顶点V0~Vw的最短路径*/
    int final[MAXVEX];
    
    /*1.初始化数据*/
    for(v=0; v<G.numVertexes; v++)
    {
        //全部顶点初始化为未知最短路径状态0
        final[v] = 0;
        //将与V0 点有连线的顶点最短路径值;
        (*D)[v] = G.arc[v0][v];
        //初始化路径数组p = 0;
        (*P)[v] = 0;
    }
    
    //V0到V0的路径为0
    (*D)[v0] = 0;
    //V0到V0 是没有路径的.
    final[v0] = 1;
    //v0到V0是没有路径的
    (*P)[v0] = -1;
    
  
    
    //2. 开始主循环,每次求得V0到某个顶点的最短路径
    for(v=1; v<G.numVertexes; v++)
    {
        
        //当前所知距离V0顶点最近的距离
        min=INFINITYC;
        /*3.寻找离V0最近的顶点*/
        for(w=0; w<G.numVertexes; w++)
        {
            if(!final[w] && (*D)[w]<min)
            {
                k=w;
                //w顶点距离V0顶点更近
                min = (*D)[w];
            }
        }
        
        //将目前找到最近的顶点置为1;
        final[k] = 1;
        
        /*4.把刚刚找到v0到v1最短路径的基础上,对于v1 与 其他顶点的边进行计算,得到v0与它们的当前最短距离;*/
        for(w=0; w<G.numVertexes; w++)
        {
            //如果经过v顶点的路径比现在这条路径长度短,则更新
            if(!final[w] && (min + G.arc[k][w]<(*D)[w]))
            {
                //找到更短路径, 则修改D[W],P[W]
                //修改当前路径的长度
                (*D)[w] = min + G.arc[k][w];
                (*P)[w]=k;
            }
        }
    }
}

Floyd算法

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。

算法描述

从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大. 对于每一对顶点u 和 v，看看是否存在一个顶点 w使得从 u 到 w再到 v比己知的路径更短。如果是更新它。

代码实现

/* 
 Floyd算法，求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]。
 Patharc 和 ShortPathTable 都是二维数组;
 */
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D)
{
    int v,w,k;
    
    /* 1. 初始化D与P 矩阵*/
    for(v=0; v<G.numVertexes; ++v)
    {
        for(w=0; w<G.numVertexes; ++w)
        {
            /* D[v][w]值即为对应点间的权值 */
            (*D)[v][w]=G.arc[v][w];
             /* 初始化P P[v][w] = w*/
            (*P)[v][w]=w;
        }
    }
    
    //2.K表示经过的中转顶点
    for(k=0; k<G.numVertexes; ++k)
    {
        for(v=0; v<G.numVertexes; ++v)
        {
            for(w=0; w<G.numVertexes; ++w)
            {
                /*如果经过下标为k顶点路径比原两点间路径更短 */
                if ((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
                {
                    /* 将当前两点间权值设为更小的一个 */
                    (*D)[v][w]=(*D)[v][k]+(*D)[k][w];
                    /* 路径设置为经过下标为k的顶点 */
                    (*P)[v][w]=(*P)[v][k];
                }
            }
        }
    }
}