话说为什么笔者我要求虐去研究什么贝塞尔曲线?讲真,我一个数学一般般,高数及格飘过的人为什么要求虐去搞数学公式啊!研究完贝塞尔曲线,我突然想好好学习数学。真的是数学不好,学什么编程啊。(哭晕在草稿纸中……)
正片干货在此:
科普时间
提到贝塞尔曲线,大家第一反应是什么?
学习CSS的小伙伴应该会知道一个叫做animation-timing-function:cubic-bezier(x1,y1,x2,y2)的参数,用于CSS动画时间的参数。如果无法理解,就假象下匀速运动和变速运动的。如果还是没感觉,就想象你在跑步机上跑步,1小时内,有时用8KM/h的速度,有时候用10KM/h的速度。也就是animation-timing-function:cubic-bezier(x1,y1,x2,y2)的意思就是让你在一定时间内,用不同的速度运动(运动方式不限,可以是平移,旋转,拉伸……)。
但是贝塞尔曲线,既然是曲线,一开始并不是用于时间函数的,而是真的用来画曲线的,比如PS中的钢笔工具。(惊喜不惊喜,意外不意外,此处应该有表情包。)
Bézier curve的定义
A Bézier curve is defined by a set of control points P0 through Pn, where n is called its order (n = 1 for linear, 2 for quadratic, etc.). The first and last control points are always the end points of the curve; however, the intermediate control points (if any) generally do not lie on the curve. The sums in the following sections are to be understood as affine combinations, the coefficients sum to 1.
笔者的渣翻译:一条贝塞尔曲线是由一组Points从P0~PN所控制的,这边N就是他的顺序(比如N=1的时候是线性的,2的时候是二次,等等)。第一个控制点和最后一个控制点是曲线的终点;然而中间的一些控制点(如果有),通常不在曲线上。这些点的组合可以理解为仿射组合(affine combination,也就是不仅有点,还有点指向的方向),他们的系数之和等于一。
通俗解释:
- 贝塞尔曲线是由
一堆点的集合绘制而成。 - 这
一堆点是在定义的P0~PN的控制之下得出的。 - P0~PN这些定义的点,第一个点和最后一个点是曲线的开头和结尾。
一条曲线的获得过程真不容易,也就是说在计算机中曲线的获得过程并不一帆风顺,并不像我们徒手画一条曲线那么简单。如果大家画过素描,应该知道一个圆应该怎么画。也许有人会说,圆这么简单,徒手就是一个大饼。对此只能说少年你太简单了。素描的圆并不是一蹴而就,而是不断地切割,通过线段慢慢地得出一个圆。当然这只是一个比喻,计算机中的曲线是通过无数的线段组合而成的。
Bézier curve的实例
假设我们将曲线分为10段,贝塞尔曲线就是通过P0~N个点控制,从P0出发,在P0~N这些点的N-1条连线中寻找线段1/10处的点,再链接新的点得出N-2条连线,寻找新得出的线段中1/10处的点,如此循环,直至只剩两点一线,在这条最终的线上寻找一个最终点,也就是组成曲线的点。然后查找2/10处的点,初次循环,直至到达PN。
是不是有点懵,一条曲线的诞生之路真艰辛。来!让我们通过实例来feel一下。我们是如何通过定义几个点来控制一条曲线的。
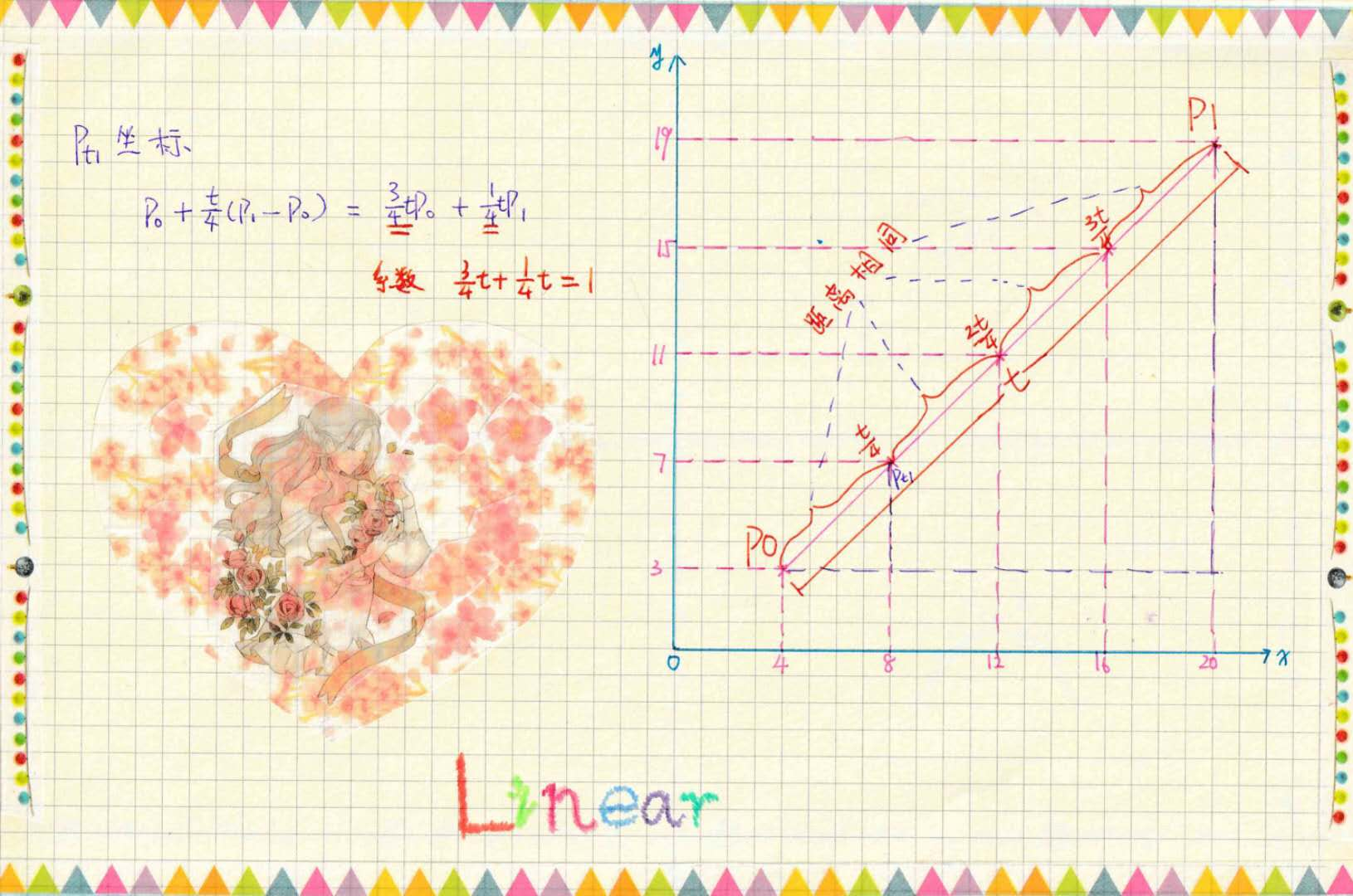
线性Bézier curves
线性Bézier curves是由两个点P0和P1控制形成的,这个是最简单的,就是初中(也许是小学了)学的一次函数。大家也许会质疑为什么我要解释这么简单的问题,笔者你是不是傻了。(放开我,我没疯,我还可以继续。)上一节提到了曲线其实是由无数的线段组成的,因此这个线性的Bézier curve当然就是基础啦!
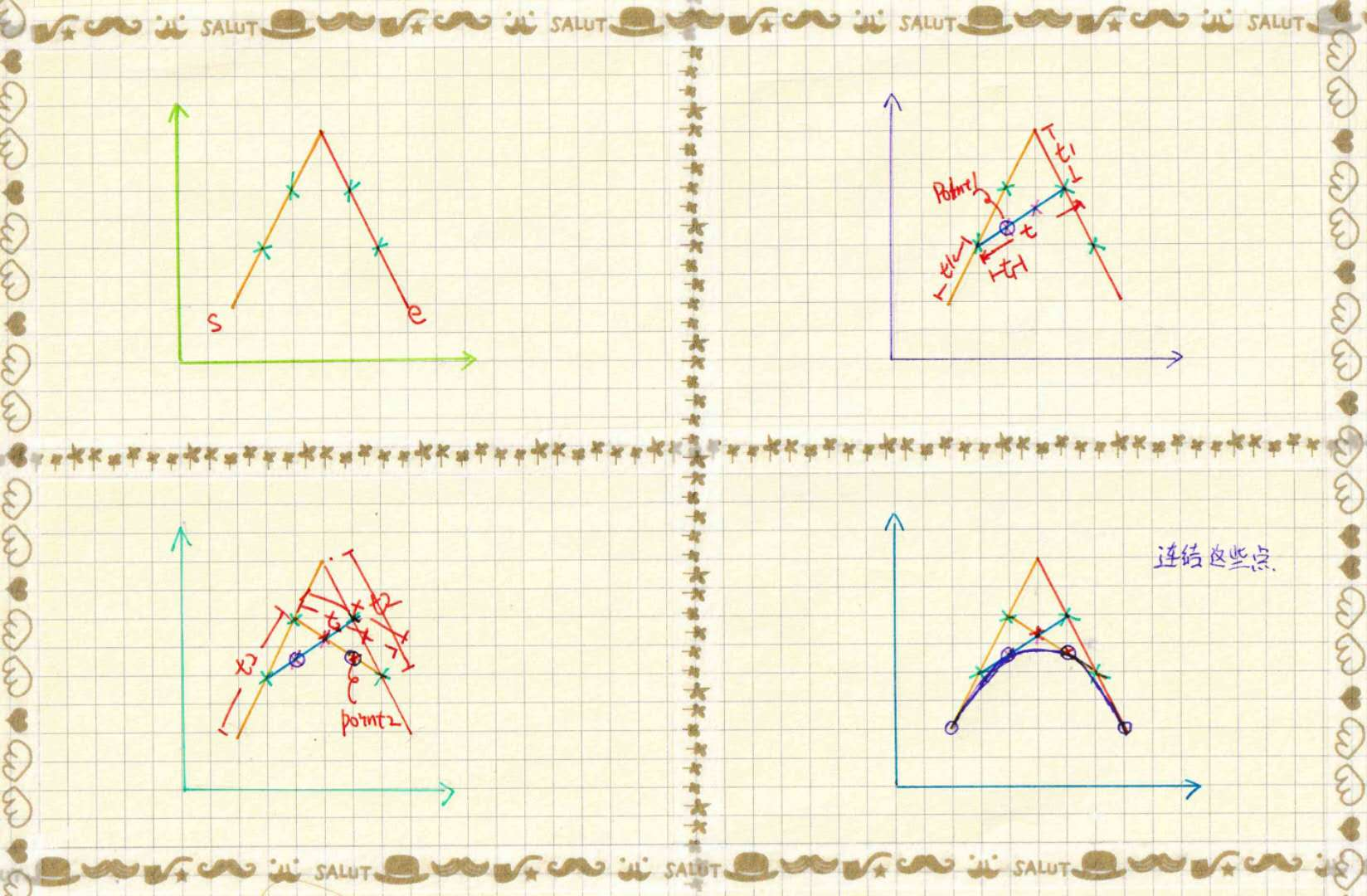
二次Bézier curves
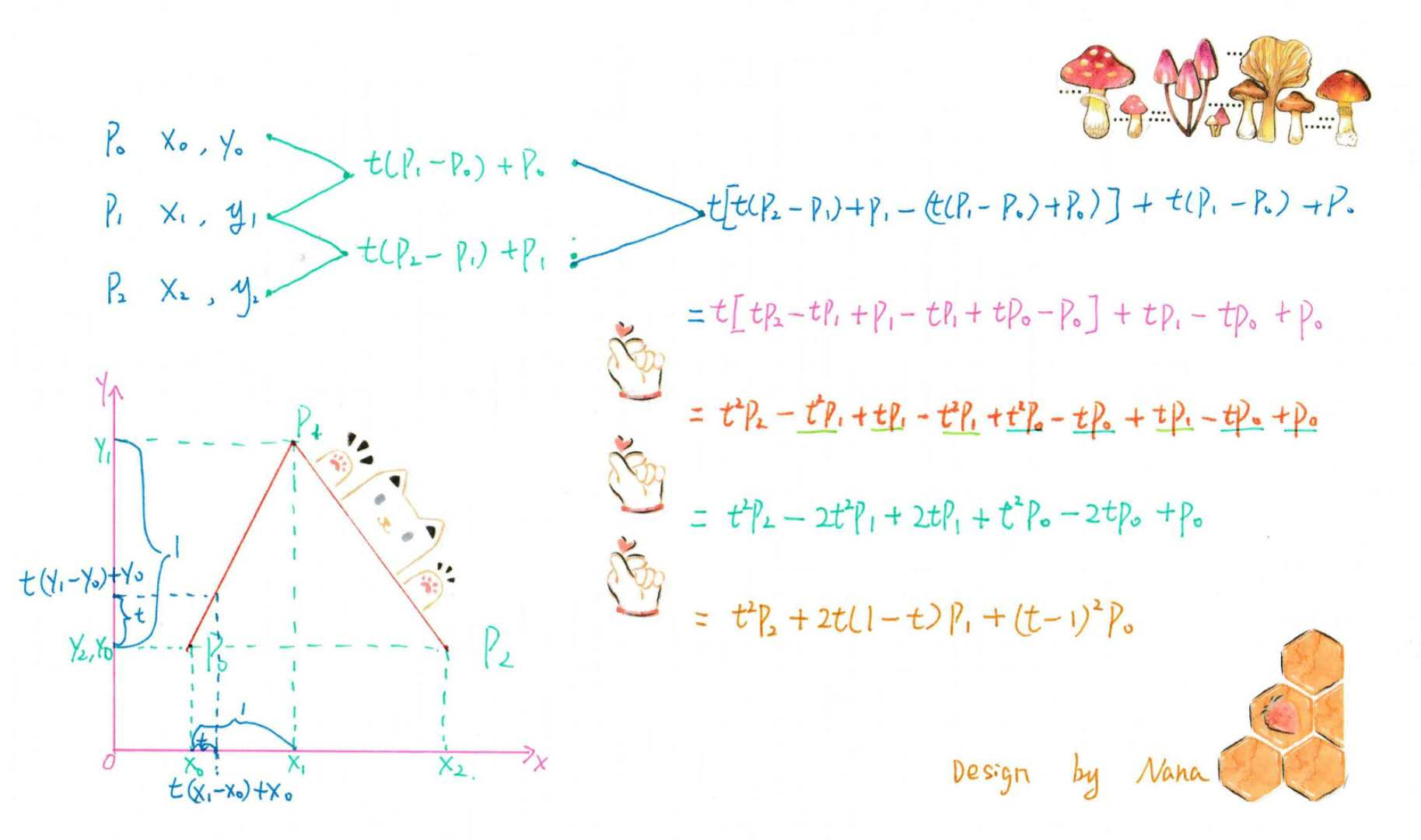
好了离开了一次函数,我们要进入二次函数了。二次Bézier curves是由三个点P0,P1和P2组成的。从这里开始,我们就要打开新世界的大门了,通过上一节简单的线性Bézier curves我们开始推导二次Bézier curves的作图方式以及数学公式。
公式推导:
三次Bézier curves
终于来到了CSS中animation-timing-function:cubic-bezier(p1x,p1y,p2x,p2y)所需要的曲线了。这个曲线,我们可以通过上述的二次依葫芦画瓢画出来,不同的是动态的线段又多了两条。
公式推导:
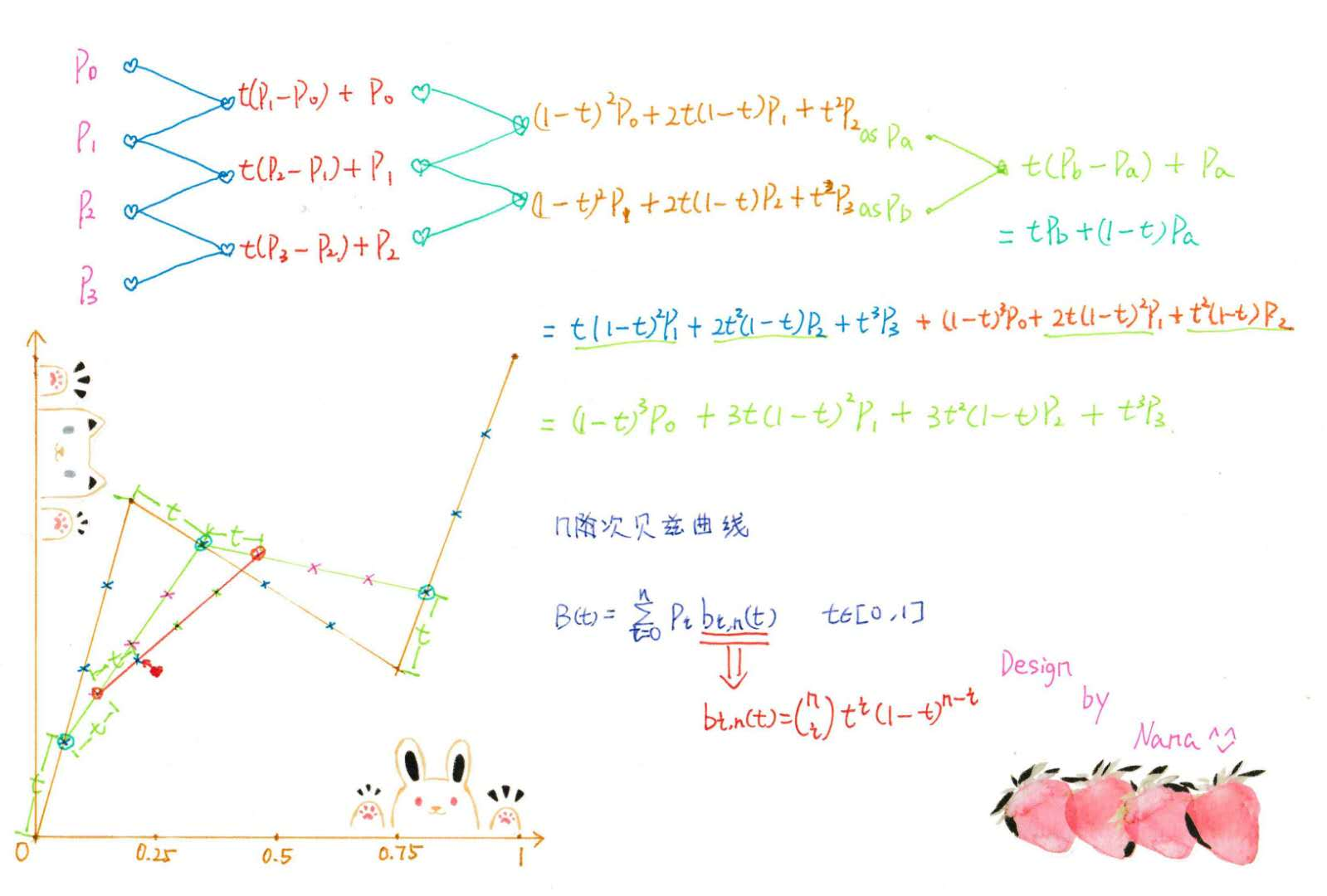
这个分解图画起来,有点凶残,所以笔者做了一个Canvas动画
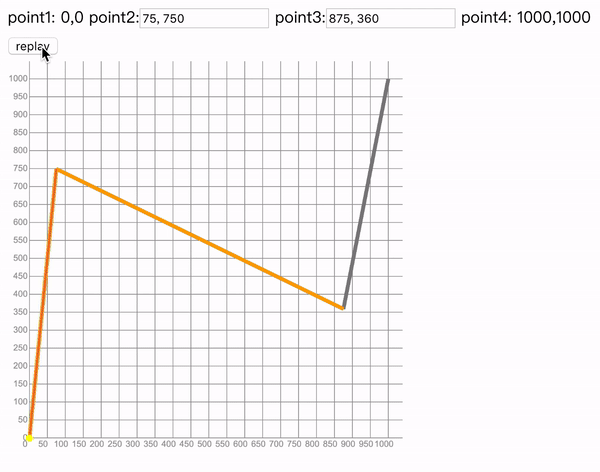
在线enjoy的地址:codepen
如果是只是使用,我们可以通过一个作弊网站获取到常用的时间曲线参数。
三次Bézier curves和CSS的时间函数的关系
相信大家都发现了上文提到的CSS中的animation-timing-function:cubic-bezier(x1,y1,x2,y2)这个属性,其实就是三次贝塞尔曲线的一个应用,不过里的第一个点和最后一个点的固定的,可以调节的之后P1和P2。
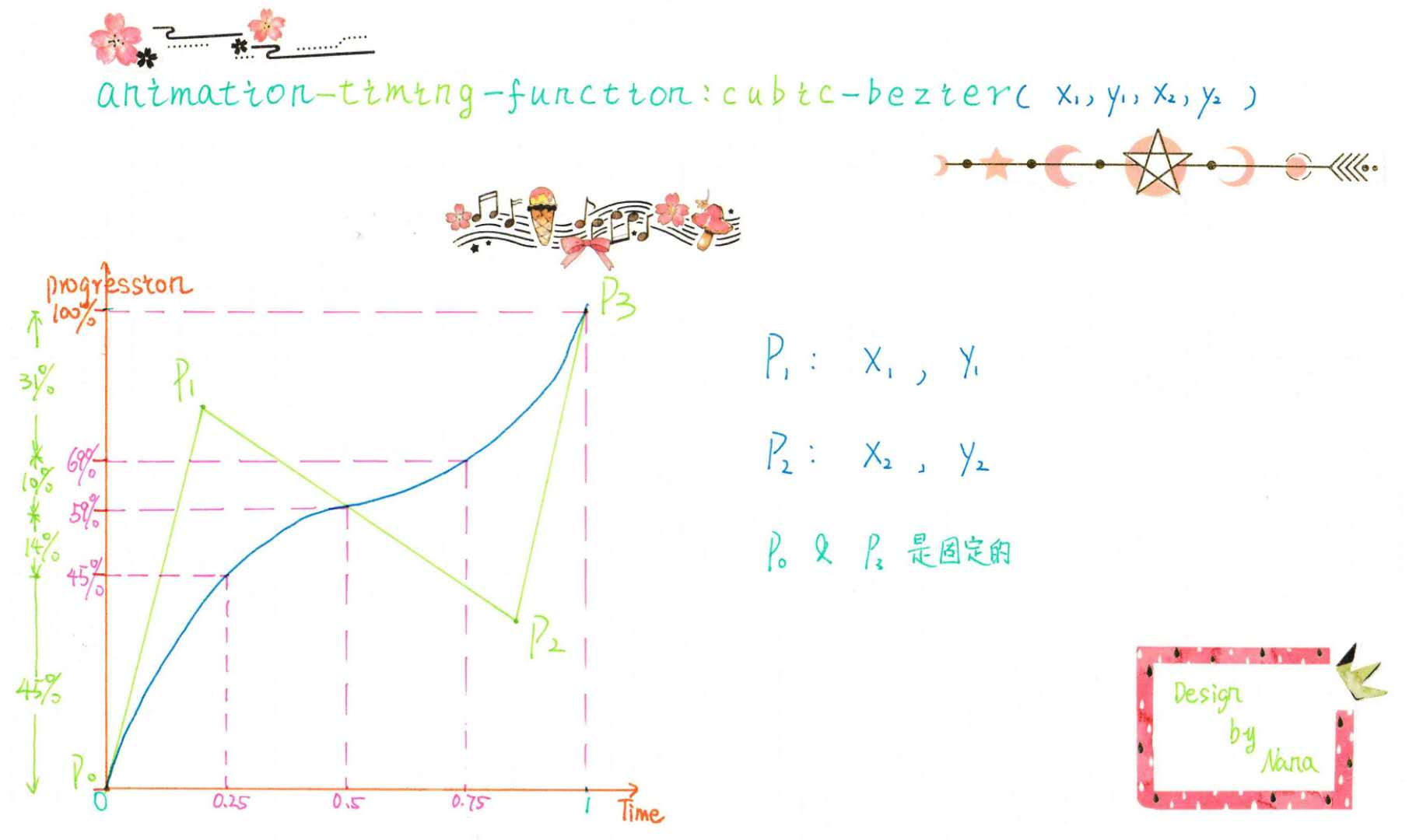
虽然绘制贝塞尔曲线不难,只要理解了其原理,画一个曲线相信都难不倒大家。但是CSS的时间函数真的难解,因为我们通常是通过时间t,来得出(x,y)的坐标,从而绘制曲线,但是在CSS的时间函数中,我们使用的可不是这个方式哦。而是通过已知的x,求出y的值。这里的难点在于,需要求解一个3元一次方程(有兴趣的可以去解三元一次方程,得出t,在带入公式得到y)。
也有大神做了这个网站供我们玩转贝塞尔曲线函数,这样就不用自己去解三元一次方程了。
递归搞定所有类型贝塞尔曲线
虽然我们可以导出公式来计算贝塞尔曲线的每个点的位置,但是我们可以用另一种更加暴力的方式来完成,也更加直观。
既然贝塞尔曲线是直线截出来,那么我就可以用递归一层层回调到只剩一个点,然后根据t再计算新的点,连接这些点我的曲线就形成啦!
每一个贝塞尔曲线都是由线性递归而来,那么先写一个线性的公式。
function linearBezierCurze(a, b, c, d){
//(a,b),(c,d)
let s1 = c - a, s2 = d - b
return function (t) {
return [
s1 * t + a,
s2 * t + b
]
}
}
接着对定位点们利用reduce计算两点之间的新的点,直至新的点只剩一个。
function drawPoints(point){
let newPoint=[]
point.reduce((p,c)=>{
newPoint.push(linearBezierCurze(...p,...c)(t))
return c
})
if(newPoint.length===1){
return newPoint[0]
}else{
return drawPoints(newPoint)
}
}
笔者写了一个在线play的demo,大家可以加多点玩,写的比较简陋,不要嫌弃:demo
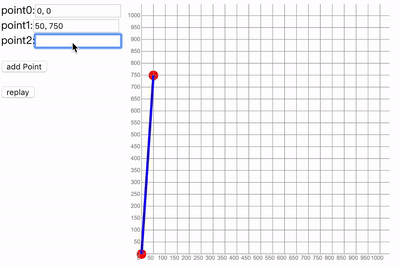
总结
笔者溜了溜了……