在一个面经中看到这个问题,正好不会,总结一下。感觉这一题如果问到数据库的时候能把这个说的比较清楚应该会很加分。要了解他们的区别,首先得了解b树的b+树分别是什么?
1. 什么是b树?是怎么实现的?
1.1 为什么需要b树和b+树
我们常用的二叉搜索树的结构是红黑树,包括面试中红黑树被问到的几率也更大。甚至STL中map和set的的实现也是红黑树,可见红黑树的强大和其广泛的适用性。那么为什么还要发明出b树呢?要回答这个问题首先先回忆一下链表这个结构,由于其中的元素是通过指针来连接的,存储并不是连续的,所以地址连续的数组的程序局部性是优于链表的。对于二叉树来说同样如此,因为是通过指针来组织的,其各个节点的地址不是连续的,因此程序的局部性并不好。
举个例子,当你要查找一个节点的时候,其key是8,那么这个key对应的value只存了一个值假设值为字符串“hello”,它被存放在内存中的页号为100的页中,因此内存就会调入页号为100的页。这是你又查找了key为9的节点,其对应的value是字符串“word”,由于红黑树节点的地址是不连续的,所以它有可能被存在离key为8的节点很远的地址,比如它被存放在页号为200的页中,因此内存又需要调入页号为200的页。假如一棵红黑树进行频繁的查找操作,那么势必就会由于地址不连续而不断的调入新的页,带来大量的IO操作。而主存访问外存的效率是极其低下的,通常是比访问主存还要慢上3个数量级,对程序的性能造成极大的影响。
相比于红黑树,b树的出现能在一定的程度上缓解频繁IO操作带来的性能损耗。那么它是怎么做到减少IO次数的呢?主要通过将多个节点的key和value存放在一个中,在这一个节点中存放的value的地址是连续的,因此在局部性上由于红黑树,从而减少IO的次数。在上面的例子中,节点8和9是两个不同的节点,因此分布在不同的,需要两次IO操作。而在b树中,有可能节点8和9存放在同一个节点中,也就可能存在在同一个页中,只需要一次IO操作。
1.2 b树的结构是怎么实现把多对key和value存放在一个节点中的?
b树是一种多路平衡的树,它的平衡是完美的平衡,即所有叶节点都在同一层。
- 根节点至少有两个子节点;
- 每个节点最多有m-1个key值,升序排列,value也按照键值排列,左边的小于key1,中间的between key1 key2,右边的大于key2;
- 除根节点外,其他节点至少有m/2取上整再减一个节点。
在实际的b树实现中,一个节点中的[m/2,m-1]个key是存成一个连续的vector的,因此对这个节点内部所有的key的访问都需要的是同一个页,而不是多个页面,从而减少IO的次数。
1.3 b树的rebanlance
对于平衡的二叉搜索树而言,除了定义balance的标准,rebanlance的算法也很重要。对于b树而言,每个节点的key的数量是有上限和下限的,在插入和删除关键码的动态操作中有可能会破坏b树的上限和下限的约束。因此就需要算法使得b树重新回到满足约束的状态就是rebalance。
- 因为插入操作而使得关键码的数量超出上限,叫做上溢。发生上溢的状态必然是原本一个节点就已经有了m-1个关键码,然后又插入了一个关键码,使得该节点的关键码数量变为m个。当发生上溢时,可以选择该节点中的中值关键码作为分界,将一个节点分裂成两个节点。得益于规则的数量,分裂后的两个节点的数量也不会发生下溢。同时中值位置的关键码则交给父节点,插入到父节点中,被分裂产生的两个新节点正好分布在其左右。对于父节点而言,等效地在其节点中插入了一个关键码。如果再次发生上溢则继续类似的操作,直到到根的位置。假如到了根的位置根也发生了上溢,则取出中值作为新的根,因而根节点会存在只有一个关键码的特殊情况。
- 因为删除操作而使得关键码的数量超出了下限,叫做下溢。发生下溢的状态必然是原本一个节点就已经只剩最低限度(m/2取上整再减一)的节点数,然后又删除了一个关键码。为了解决该节点的下溢,首先会考虑从其左右兄弟中借一个节点使得该节点满足节点数的下限。因此只要其左兄弟或者右兄弟中有可以借出的节点(可借出的节点是只借出后不会发生下溢,如果是其左兄弟,则借出做兄弟中的最大值,如果是右兄弟则是最小值),就可以通过借一个节点来解决下溢。但是为了保持b树的顺序性,并不是直接把兄弟借出的关键码合并到自己的节点中,而是把兄弟节点的关键码提到父节点中,在从父节点中拿出一个合适的关键码合并到自己的节点中。这个合适的关键码就是该节点和其兄弟节点之间的那个关键码,被提上去的那个关键码则会取代这个位置。另外一种情况就是兄弟节点中也没有可借出的节点了,这时候只能选择合并,由于兄弟节点中也无可借出的节点,因此它们合并也不会超过上限,为了保持顺序性,合并的过程中,两兄弟之间的那个在父节点中的关键码也需要合并进来。如此一来,父节点也可以等效地看成是删除了一个节点。如果再次发生下溢,依然可以用同样的办法解决下溢。
总结下来就是上溢时节点分裂,以中值为分界分裂,中值关键码插入父节点;下溢时先尝试从兄弟节点借一个关键码,没有可借的就和兄弟合并。
2. 什么是b+树?以及和b树的区别
2.1 什么是b+树
B+树和B树类似,但多了几条规则:
- 非叶子结点的子树指针个数与关键字(节点中的元素个数)个数相同
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间)
- 所有叶子结点有一个链指针
- 所有关键字都在叶子结点出现
- 只有叶子节点有Data域
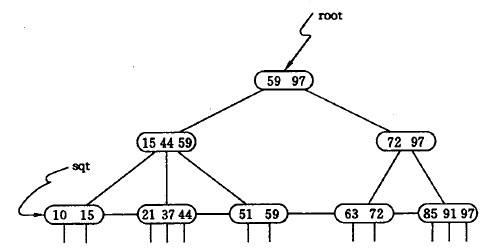
如图,以上规则的目的主要是为了把所有的关键码都集中在叶节点处,其他节点仅仅只用来索引到叶节点,因此不必包含data域。叶节点还链接成了一个链表,主要是为了方便范围查询。
B+树和B树的操作的优势在于B+树的查找效率上:
- B树中每个节点的关键字都有data域,而B+树除了叶子节点,其他节点只有索引,也就是说同样的磁盘页B+树可以容纳更多的节点。
- B+树的范围查询更加方便,可以先找到范围下限,然后通过叶子结点的链表顺序遍历,直至找到上限即可。而B树只能先找到下限,通过中序遍历查找,直到找到上限。