为求方便节点存储数据类型默认为char,未以模板形式实现
1 节点结构
struct BNode {
char data;
BNode *lChild, *rChild;
BNode(char a) {
data = a;
}
};
2 二叉树的创建
2.1.使用带终止符的前序遍历创建
必须对应二又树结点前序遍历的顺序,并约定以输入序列中不可能出现的值作 为空结点的值以结束递归,此值通过构造函数存放在RefValue中。例如用“#”或表示字符序列或正整数序列空结点。
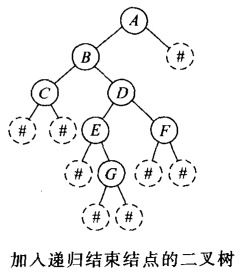
算法的基本思想:
每读入一个值,就为它建立结点。该结点作为根结点,其地址通过函数的引用型参数subTree直接链接到作为实际参数的指针中。然后,分别对根的左、右子树递归地建立子树,直到读入“#”建立空子树递归结束。
///前序遍历创建二叉树(带中止标记)
void CreateBinTree_UsePreFlag(){
cout << "please input preOrder number with refuse value: " << endl;
CreateBinTree_UsePreFlag(root);
}
void CreateBinTree_UsePreFlag(BNode* &subTree) { //传入的指针一定要是引用,否则无法修改传入指针的指向位置
char item;
if (cin >> item)
{
if (item != refuseValue)
{
subTree = new BNode(item);
CreateBinTree_UsePreFlag(subTree->lChild);
CreateBinTree_UsePreFlag(subTree->rChild);
}
else {
subTree = NULL;
}
}
}
2.2 使用广义表创建
从广义表A(B(D,E(G,)),C(,F))# 建立起来的二叉树。
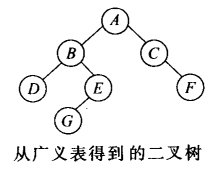
1.若是字母(假定以字母作为结点的值),则表示是结点的值,为它建立一个新的结点,并把该结点作为左子女(当k=1)或右子女(当k=2)链接到其父结点上。
2.若是左括号"(",则表明子表的开始,将k置为1;若遇到的是右括号")",则表明子表结束。
3.若遇到的是逗号",",则表示以左子女为根的子树处理完毕,应接着处理以右子女为根的子树,将k置为2。如此处理每一个字符,直到读入结束符“#”为止。
在算法中使用了一个栈s,在进入子表之前将根结点指针进栈,以便括号内的子女链接之用。在子表处理结束时退栈。
///使用广义表创建
void CreateBinTree_UseGenTable() {
cout << "please input Generalized table: " << endl;
CreateBinTree_UseGenTable(root);
}
///使用广义表创建二叉树函数,这里以“字符”创建二叉树,以'#'字符代表结束
void CreateBinTree_UseGenTable(BNode* &BT)
{
stack<BNode*> s;
BT = NULL;
BNode *p, *t; //p用来记住当前创建的节点,t用来记住栈顶的元素
int k; //k是处理左、右子树的标记
char ch;
while (1)
{
cin >> ch;
if (ch == refuseValue)
break;
switch (ch)
{
case '(': //对(做处理
s.push(p);
k = 1;
break;
case ')': //对)做处理
s.pop();
break;
case ',': //对,做处理
k = 2;
break;
default:
p = new BNode(ch); //构造一个结点,!注意要给新节点的左右孩子指针赋空值!
p->lChild = NULL;
p->rChild = NULL;
if (BT == NULL) //如果头节点是空
{
BT = p;
}
else {
if (k == 1) //链入*t的左孩子
{
t = s.top();
t->lChild = p;
}
else //链入*t的右孩子
{
t = s.top();
t->rChild = p;
}
}
}
}
}
2.3 使用前序遍历和中序遍历创建
算法思路:
根据前序遍历,先找到这棵树的根节点,也就是数组受中第一个结点的位置,创建根节点。然后在中序遍历中找到根的值所在的下标,切出左右子树的前序和中序。
注意:如果前序遍历的数组长度为0,说明是一棵空树。
///使用先序遍历和中序遍历创建
void CreateBinTree_Pre_mid() {
char pre[50];
char mid[50];
cout << "please input preOrder: " << endl;
cin >> pre;
cout << "please input midOrder: " << endl;
cin >> mid;
string s1(pre);
string s2(mid);
if (s1.length() != s2.length()) {
cout << "error input!" << endl;
return;
}
int n = s1.length();
CreateBinTree_Pre_mid(root,pre,mid,n);
}
void CreateBinTree_Pre_mid(BNode *&cur, const char *pre, const char *mid, int n) {
if (n <= 0)
{
cur = NULL;
return;
}
int k = 0;
while (pre[0] != mid[k]) {
k++;
}
cur = new BNode(mid[k]); //创建结点
CreateBinTree_Pre_mid(cur->lChild, pre + 1, mid,k);
CreateBinTree_Pre_mid(cur->rChild, pre + k + 1, mid + k + 1,n-k-1);
}
2.4 使用后续遍历和中序遍历创建
算法思路:
根据后序遍历,先找到这棵树的根节点的值,也就是数组中最后一个节点(数组长度-1)的位置,由此创建根节点。然后在中序遍历中找到根的值所在的下标,切出左右子树的后续和中序。
注意:如果后序遍历的数组长度为0,说明是一棵空树。
///使用后序遍历和中序遍历创建(与上方法类似)
void CreateBinTree_post_mid() {
char post[50];
char mid[50];
cout << "please input postOrder: " << endl;
cin >> post;
cout << "please input midOrder: " << endl;
cin >> mid;
string s1(post);
string s2(mid);
if (s1.length() != s2.length()) {
cout << "error input!" << endl;
return;
}
int n = s1.length();
CreateBinTree_post_mid(root, post, mid, n);
}
///后序遍历和中序遍历创建二叉树
void CreateBinTree_post_mid(BNode* &cur, const char *post, const char *mid, int n) {
if (n <= 0)
{
cur = NULL;
return;
}
int k = 0;
while (post[n - 1] != mid[k]) {
k++;
}
cur = new BNode(mid[k]);
CreateBinTree_post_mid(cur->lChild, post, mid, k);
CreateBinTree_post_mid(cur->rChild, post + k, mid + k+1,n-k-1);
}
3 二叉树的遍历
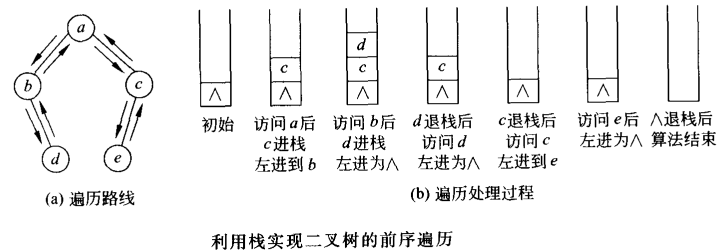
3.1 先序遍历
非递归遍历算法思路: 为了把一个递归过程改为非递归过程,一般需要利用一个工作栈,记录遍历时的回退路径。
///先序遍历
void preOrder() {
cout << "preOrder num: ";
//递归遍历
// preOrderPrint_UseRecursion(root);
//使用栈遍历
// preOrderPrint_UseStack1();
preOrderPrint_UseStack2();
cout << endl;
}
//1 递归遍历
void preOrderPrint_UseRecursion(BNode* subTree) {
if (subTree != NULL) {
cout << subTree->data << " ";
preOrderPrint_UseRecursion(subTree->lChild);
preOrderPrint_UseRecursion(subTree->rChild);
}
}
//2.1 利用栈实现前序遍历的过程。每次访问一个结点后,在向左子树遍历下去之前,利用这个栈记录该结点的右子女(如果有的话)结点的地址,
//以便在左子树退回时可以直接从栈顶取得右子树的根结点,继续其右子树的前序遍历。
void preOrderPrint_UseStack1() {
stack<BNode*> s;
BNode* p=root;
s.push(NULL);
while (p != NULL) {
cout << p->data << " ";
if (p->rChild != NULL)
s.push(p->rChild);
if (p->lChild != NULL)
{
p = p->lChild; //把当前还未处理的右孩子指针存起来
}
else {
p = s.top();
s.pop();
}
}
cout << endl;
}
//2.2 为了保证先左子树后右子树的顺序,在进栈时是先进右子女结点地址,后进左子女结点地址,出栈时正好相反。
void preOrderPrint_UseStack2() {
BNode* p = root;
stack<BNode*> s;
s.push(p);
while (!s.empty()) {
p = s.top();
s.pop();
cout << p->data << " ";
if (p->rChild != NULL)
s.push(p->rChild);
if(p->lChild!=NULL)
s.push(p->lChild);
}
cout << endl;
}
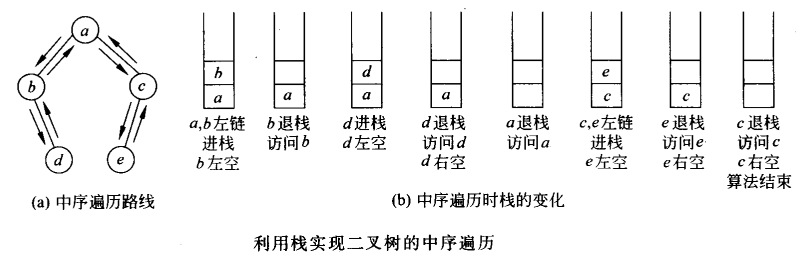
3.2 中序遍历
非递归算法思路:
需要使用一个栈,以记录遍历过程中回退的路径。在一棵子树中首先访问的是中序下的第一个结点,它位于从根开始沿leftChild链走到最左下角的结点,该结点的leftChild指针为NULL。访问它的数据之后,再遍历该结点的右子树。此右子树又是二叉树,重复执行上面的过程,直到该子树遍历完。
void midOrder() {
cout << "midOrder num: ";
///递归遍历
midOrderPrint_UseRecursion(root);
///使用栈遍历
// midOrderPrint_UseStack();
cout << endl;
}
//1.递归进行遍历
void midOrderPrint_UseRecursion(BNode* subTree) {
if (subTree != NULL) {
midOrderPrint_UseRecursion(subTree->lChild);
cout << subTree->data << " ";
midOrderPrint_UseRecursion(subTree->rChild);
}
}
//2.使用栈进行遍历
void midOrderPrint_UseStack() {
BNode* p = root;
stack<BNode*> s;
do{
while (p != NULL) {
s.push(p);
p = p->lChild;
}
if (!s.empty()) {
p = s.top();
s.pop();
cout << p->data << " ";
p = p->rChild;
}
} while (p != NULL || !s.empty());
}
3.3 后续遍历
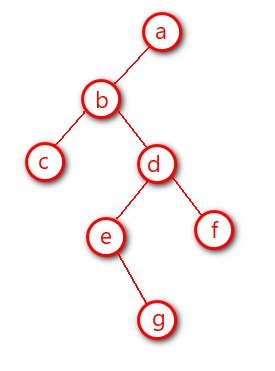
1、如果栈顶元素非空且左节点存在,将其压入栈中,如果栈顶元素存在左节点,将其左节点压栈,重复该过程。直到左结点不存在则进入第2步。
2、判断上一次出栈节点是否是当前栈顶结点的右节点(就是右叶子结点,如:g,f结点),或者当前栈顶结点不存在右结点(如:g,f,a结点),将当前节点输出,并出栈。否则将当前栈顶结点右孩子节点压栈,再进入第1步。
///后序遍历
void postOrder() {
cout << "postOrder num: ";
//递归遍历
// postOrderPrint_UseRecursion(root);
//使用栈遍历
postOrderPrint_UseStack();
cout << endl;
}
//1.递归进行遍历
void postOrderPrint_UseRecursion(BNode* subTree) {
if (subTree != NULL) {
postOrderPrint_UseRecursion(subTree->lChild);
postOrderPrint_UseRecursion(subTree->rChild);
cout << subTree->data << " ";
}
}
//2.使用栈进行遍历
void postOrderPrint_UseStack() {
if (root == NULL)
return;
BNode *p = root;
stack<BNode *> s;
s.push(p);
BNode *lastPop = NULL;
while (!s.empty())
{
while (s.top()->lChild != NULL)
s.push(s.top()->lChild);
while (!s.empty())
{
//右叶子结点 || 没有右结点
if (lastPop == s.top()->rChild || s.top()->rChild == NULL)
{
cout << s.top()->data << " ";
lastPop = s.top();
s.pop();
}
else if (s.top()->rChild != NULL)
{
s.push(s.top()->rChild);
break;
}
}
}
}
3.4 先序遍历(广义表形式输出)
///先序遍历,广义表形式
void preOrder_GenTable() {
cout << "preOrder num with generalize table: ";
GenTablePrint(root);
cout << endl;
}
///二叉树以广义表形式输出
void GenTablePrint(BNode *BT)
{
if (BT != NULL) //树为空时结束递归
{
cout << BT->data;
if (BT->lChild != NULL || BT->rChild != NULL)
{
cout << '(';
if (BT->lChild != NULL)
{
GenTablePrint(BT->lChild);
}
cout << ',';
if (BT->rChild != NULL)
{
GenTablePrint(BT->rChild);
}
cout << ')';
}
}
}
3.5 层次遍历
算法思路:
按层次顺序访问二叉树的处理需要利用一个队列。在访问二又树的某一层结点时,把下一层结点指针预先记忆在队列中,利用队列安排逐层访问的次序。因此,每当访问一个结点时,将它的子女依次加到队列的队尾,然后再访问已在队列队头的结点。这样可以实现二又树结点的按层访问。
///层次遍历(使用队列实现)
void levelOrderPrint() {
BNode* p = root;
queue<BNode*> Queue;
Queue.push(p);
while (1) {
if(p->lChild!=NULL)
Queue.push(p->lChild);
if (p->rChild != NULL)
Queue.push(p->rChild);
cout << p->data << " ";
Queue.pop();
if (Queue.empty())
break;
else
p = Queue.front();
}
}
4 其他重要成员函数
4.1 获取根节点
BNode* getRoot() {
return root;
}
4.2 获取二叉树节点数量
int size() { //二叉树大小
return size(root);
}
///节点p开头的子树节点数目
int size(BNode* p) {
if (p == NULL)
return 0;
return 1 + size(p->lChild) + size(p->rChild);
}
4.3 获取二叉树高度
int height() {
//return height_UseStack(root);
return height_UseRecursion(root);
}
///节点p开头的子树节点高度
int height_UseRecursion(BNode *p)
{
if (p == NULL)
return 0;
int i = height_UseRecursion(p->lChild);
int j = height_UseRecursion(p->rChild);
return i > j ? i + 1 : j + 1;
}
int height_UseStack(BNode *T) {
if (!T)
return 0;
int front = -1, rear = -1;
int last = 0, level = 0;
BNode* tree[100];
tree[++rear] = T;
BNode* p;
while (front < rear) {
p = tree[++front];
if (p->lChild != 0)
tree[++rear] = p->lChild;
if (p->rChild != NULL)
tree[++rear] = p->rChild;
if (front == last)
{
level++;
last = rear;
}
}
return level;
}
4.4 寻找某个节点的父节点
//从结点subTree开始,搜索结点current的父节点,找到返回父节点的地址,找不到返回NULL
BNode* parent(BNode* subTree, BNode* current) {
if (subTree == NULL)
return NULL;
if (subTree->lChild == current || subTree->rChild == current)
return subTree;
BNode* p;
if ((p = parent(subTree->lChild, current)) != NULL)
return p;
else
return parent(subTree->rChild, current);
}
4.5 销毁二叉树并回收空间
void destroy(BNode *p) {
if (p == NULL)
return;
else {
destroy(p->lChild);
destroy(p->rChild);
delete p;
p = NULL;
}
}
4.6 判断两个二叉树是否一致(静态函数)
static bool equal(BNode* a, BNode *b) {
if (a == NULL&&b == NULL)
return true;
if (a != NULL&&b != NULL && (a->data == b->data) && equal(a->rChild, b->rChild) && equal(a->lChild, b->lChild))
return true;
else
return false;
}
4.7 判断是否是完全二叉树
///判断是否是完全二叉树_方法1 使用层次遍历,h-1层的最后一个节点序号为pow(2, level - 1) - 1
bool isFullBinaryTree_1() {
BNode *T = root;
if (!T)
return true;
int front = -1, rear = -1;
int last = 0, level = 0;
BNode* a[100];
stack<int> frontHistory;
a[++rear] = T;
BNode* p;
while (front < rear) {
p = a[++front];
if (p->lChild != NULL)
a[++rear] = p->lChild;
if (p->rChild != NULL)
a[++rear] = p->rChild;
if (front == last) {
last = rear;
level++;
frontHistory.push(front);
}
}
frontHistory.pop();
//只需要验证h-1层最后一个节点序号是否是2^(h-1)-1即可!
return (frontHistory.top()+1) == (pow(2, level - 1) - 1);
}
///判断是否是完全二叉树_方法2 利用性质:层次遍历时出现一个叶子节点则后面的均为叶子节点(空节点)
bool isFullBinaryTree_2() {
BNode* p = root;
queue<BNode*> que;
que.push(p);
while (!que.empty()) {
p = que.front();
que.pop();
if (p) {
que.push(p->lChild);
que.push(p->rChild);
}
else {
while (!que.empty())
{
p = que.front();
que.pop();
if (p)
return false;
}
}
}
return true;
}
4.8 交换节点p为根节点的子树的所有的左右节点
///交换节点p为根节点的子树的所有的左右节点(层次遍历)
void swapLeftAndRight(BNode* p) {
// BNode* p = root;
if (!p)
return;
queue<BNode*> que;
que.push(p);
while (!que.empty()) {
p = que.front();
que.pop();
if (p->lChild != NULL)
que.push(p->lChild);
if (p->rChild != NULL)
que.push(p->rChild);
swap(p);
}
}
4.9 输出中序遍历的第i个值,其他遍历方法类似
void valueOfMidOrderNo(int i) {
int No = 0;
recursiveMidOrderTemp(root, i,No);
}
///输出中序遍历的第n的节点的值
void recursiveMidOrderTemp(BNode * subTree, int i, int &No) {//No需要所有递归部分共同维护
if (subTree != NULL) {
recursiveMidOrderTemp(subTree->lChild, i, No);
// cout << subTree->data << " ";
No++;
if (No == i) {
cout << subTree->data << endl;
return;
}
if (No > i)
return;
recursiveMidOrderTemp(subTree->rChild, i, No);
}
}
4.10 递归遍历寻找顶点到节点值为X的路径(此为逆序输出)
void printWayToX(char x) {
//printWayToX_UseRecursion(root, x);
printWayToX_UseStack(root, x);
cout << endl;
}
//1.使用递归实现
bool printWayToX_UseRecursion(BNode* p, char x) {
if (!p)
return false;
if (printWayToX_UseRecursion(p->lChild, x) || printWayToX_UseRecursion(p->rChild, x))
{
cout << p->data;
return true;
}
else if (p->data == x)
{
cout << p->data;
return true;
}
else {
return false;
}
}
//2.非递归遍历寻找。使用后序遍历,当查找到x时,栈中元素即为x的祖节点
void printWayToX_UseStack(BNode* p, char x) {
stack<BNode*> s;
BNode* lastPos = NULL;
s.push(p);
while (!s.empty()) {
while (s.top()->lChild != NULL)
{
s.push(s.top()->lChild);
//节点值为x的节点入栈后,直接将栈中元素全部输出然后退出该函数
if (s.top()->data == x) {
while (!s.empty()) {
cout << s.top()->data << " ";
s.pop();
}
return;
}
}
while (!s.empty())
{
if (lastPos == s.top()->rChild || s.top()->rChild == NULL)
{
lastPos = s.top();
s.pop();
}
else if (s.top() != NULL)
{
s.push(s.top()->rChild);
//查找到x时,直接将栈中元素全部输出然后退出该函数
if (s.top()->data == x) {
while (!s.empty()) {
cout << s.top()->data << " ";
s.pop();
}
return;
}
break;
}
}
}
}
4.11 找到值为 x 和 y的最近公共祖先节点。先分别利用后序查找x y的祖先节点存储在栈中,再在两个栈中查找最近相同节点!
char ClosestAncestorNode(char x, char y) {
if (root == NULL)
return '#';
stack<BNode*> s1,s2;
AncestorsNodeStack(x,s1);
AncestorsNodeStack(y,s2);
if (s1.empty() || s2.empty())
return '#';
int n = 0;
if (s1.size() >= s2.size())
{
n = s1.size() - s2.size();
for (int i = 0; i < n; i++)
s1.pop();
}
else {
n = s2.size() - s1.size();
for (int i = 0; i < n; i++)
s2.pop();
}
while (!s1.empty()) {
if (s1.top()->data == s2.top()->data)
return s1.top()->data;
s1.pop();
s2.pop();
}
return '#';
}
///返回存储节点值为x的祖先节点的栈
void AncestorsNodeStack(char x, stack<BNode*> &s)
{
if (root == NULL)
return;
BNode* lastPos = NULL;
s.push(root);
while (!s.empty()) {
while (s.top()->lChild != NULL)
{
s.push(s.top()->lChild);
//节点值为x的节点入栈后,中止该函数
if (s.top()->data == x)
return;
}
while (!s.empty())
{
if (lastPos == s.top()->rChild || s.top()->rChild == NULL)
{
lastPos = s.top();
s.pop();
}
else if (s.top() != NULL)
{
s.push(s.top()->rChild);
//查找到x时,中止该函数
if (s.top()->data == x)
return;
break;
}
}
}
}
4.12 二叉树的最大宽度(节点最多的一层的节点数)
int WidthOfBTree() {
if (root == NULL)
return 0;
int maxWidth = 0;
int front, rear;
front = rear = -1;
int last = 0;
BNode* p = root;
BNode* a[100];
a[++rear] = p;
while (front < rear) {
p=a[++front];
if (p->lChild != NULL)
a[++rear] = p->lChild;
if (p->rChild != NULL)
a[++rear] = p->rChild;
if (front == last)
{
last = rear;
if (rear - front > maxWidth)
maxWidth = rear - front;
}
}
return maxWidth;
}
5 参考资料
1.WindSun. 二叉树的详细实现 (C++):www.cnblogs.com/WindSun/p/1…
2.二叉树.百度百科:baike.baidu.com/item/二叉树/16…