考考你,System.out.println(1.0f - 0.9f)结果是什么?
3...
2...
1...
揭晓答案:0.100000024
如果好奇为什么答案不是0.1,就往下看⬇️

计算机科学中是怎么表示浮点数的?
我们都知道,在数学中,采用科学计数法来近似表示一个极大或极小且位数较多的数。科学计数法的表示形如:
a x 10^n. 其中1≦ |a| ≦ 10,a 称为有效数字
从数学世界的科学计数法映射到计算机世界的浮点数时,考虑到内存硬件设备的实现以及数制的变化(从十进制改为二进制),表现出来的形式略有不同。
其中,十进制中的指数变成了“阶码”,有效数字被改成了“尾数”,再加上计算机二进制数制下特有的符号位,就构成了计算机科学计数法中的三要素:
- 符号位
- 阶码位
- 尾数位
这么说可能不够直观,我们以单精度浮点数为例,它占有4个字节,总共32位,三要素表现如下:

我们一个一个来看:
-
符号位
占据最高的二进制位,0表示正数,1表示负数。
-
阶码位
符号位右侧8位用来表示指数,首先明确一点,在计算机世界主流的
IEEE754标准中,阶码位存储的是指数对应的移码。根据百度百科对于
移码的定义:得[X]移 = x + 2^n-1(n为x的二进制位数,含符号位置,在阶码的表示中,n = 8)
-
尾数位
上面说了,尾数位表示的是浮点数的有效数字。一个符合规格化的尾数位最高位一定是1(你品,你细细品...),所以为了节约存储空间,就将这个最高位1省略了。因此,尾数位真正占用的尾数是24位,表现出来23位。
介绍完三要素,我们举几个简单的例子来详细说明一下以上的知识点,比如,十进制数字“8.0”在计算机世界上的表示:
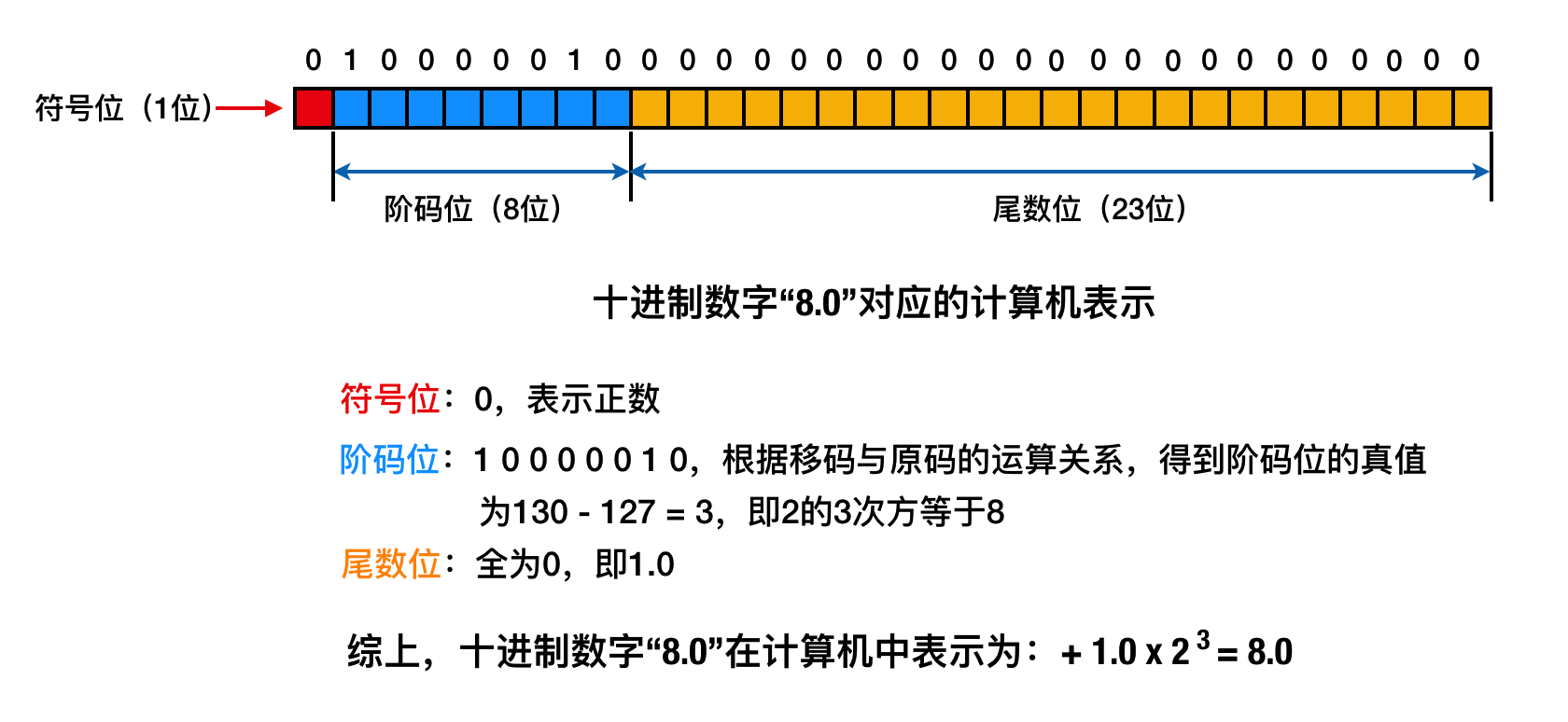
看到这里,你能很轻易的一隅三反:

那我考考你,十进制数字“0.9”怎么表示呢?
揭晓答案:

举这个例子只是为了告诉你:
某些浮点数无法在有限的二进制科学计数法中精确表示。
浮点数的加减运算
考考你,我们上小学时是怎么运算小数的加减运算的(把大象关进冰箱,统共分几步)?
1.计算小数加、减法,先把各数的小数点对齐(也就是把相同数位上的数对齐)
2.再按照整数加、减法的法则进行计算,最后在得数里对齐横线上的小数点点上小数点。
从上面我们也不难看出,小数加减法运算最重要的一个步骤就是小数点对齐。同样,对于浮点数的加减运算,“对齐小数点”也是很重要的环节。映射到科学计数法表示下的浮点数计算,就是要确保指数一样,这步操作有个专业术语,叫作对阶操作:
首先求出两浮点数阶码的差,即⊿E=Ex-Ey,将小阶码加上⊿E,使之与大阶码相等,同时将小阶码对应的浮点数的尾数右移相应位数,以保证该浮点数的值不变。
- 对阶的原则是小阶对大阶,之所以这样做是因为若大阶对小阶,则尾数的数值部分的高位需移出,而小阶对大阶移出的是尾数的数值部分的低位,这样损失的精度更小。
- 若⊿E=0,说明两浮点数的阶码已经相同,无需再做对阶操作了。
在进行对阶操作前,会首先检查参与运算的两个数是否有值为0的。因为浮点数的运算很复杂,在Google的《Performance tips》中也有一条tip:
Avoid using floating-point
当其中一个数为0时,将直接返回参与计算的另外一个值作为结果。
对阶操作完成后将尾数进行相应的运算(加法直接求和,如果是负数就先转换为补码再进行求和运算),与十进制运算类似。
经过上面的步骤得出的结果如果仍然满足
a x 2^n. 其中1≦ |a| ≦ 2的话就无需处理,如果不满足的话,就需要移动尾数的位数(左移或者右移)使其满足该形式,这一步同样会损失精度,这一步称之为结果规格化,尾数右移就叫右规,左移就叫左规。
为了弥补对阶操作以及结果规格化过程中的精度损失,会将移出的这部分数据保存起来,这就是保护位,等到结果规格化后再根据保护位进行舍入处理。
总结下来,大概就是以下几个流程:

理清楚了以上的概念,我们再来研究下标题提出的问题:
1 - 0.9 ≠ 0.1, 这是为什么?
1-0.9怎么就不等于0.1了?
首先,我们要清楚,计算机中的减法往往是转换成加法来运算的。比如 1.0 - 0.9,就等价于 1.0 + (-0.9)。
我们首先把1.0 与 -0.9 的二进制编码写出来:

上文写到过,尾数位的最高位隐藏了一位1(没记住的好好反省下),所以1.0的实际尾数为:
1000 - 0000 - 0000 - 0000 - 0000 - 0000
-0.9的实际尾数为:
1110 - 0110 - 0110 - 0110 - 0110 - 0110
接下来我们按照零值检测 -> 对阶操作 -> 尾数求和 -> 结果规格化 -> 结果舍入来操作一下:
零值检测
很明显,两个数大小都不为0,该步骤跳过。
对阶操作
1.0的阶码为127,-0.9的阶码为126,通过比较我们能够发现,-0.9的尾数的补码需要向右移动,高位补1,使其阶码变为127,达到“小数点对齐的效果”,-0.9移动后的尾数位的补码为:
1000 - 1100 - 1100 - 1100 -1100 - 1101
尾数求和
将1.0与-0.9的尾数为转换成补码,然后按位相加(对阶操作完成后,阶码位不再参与运算,只有尾数位与符号位参与运算):
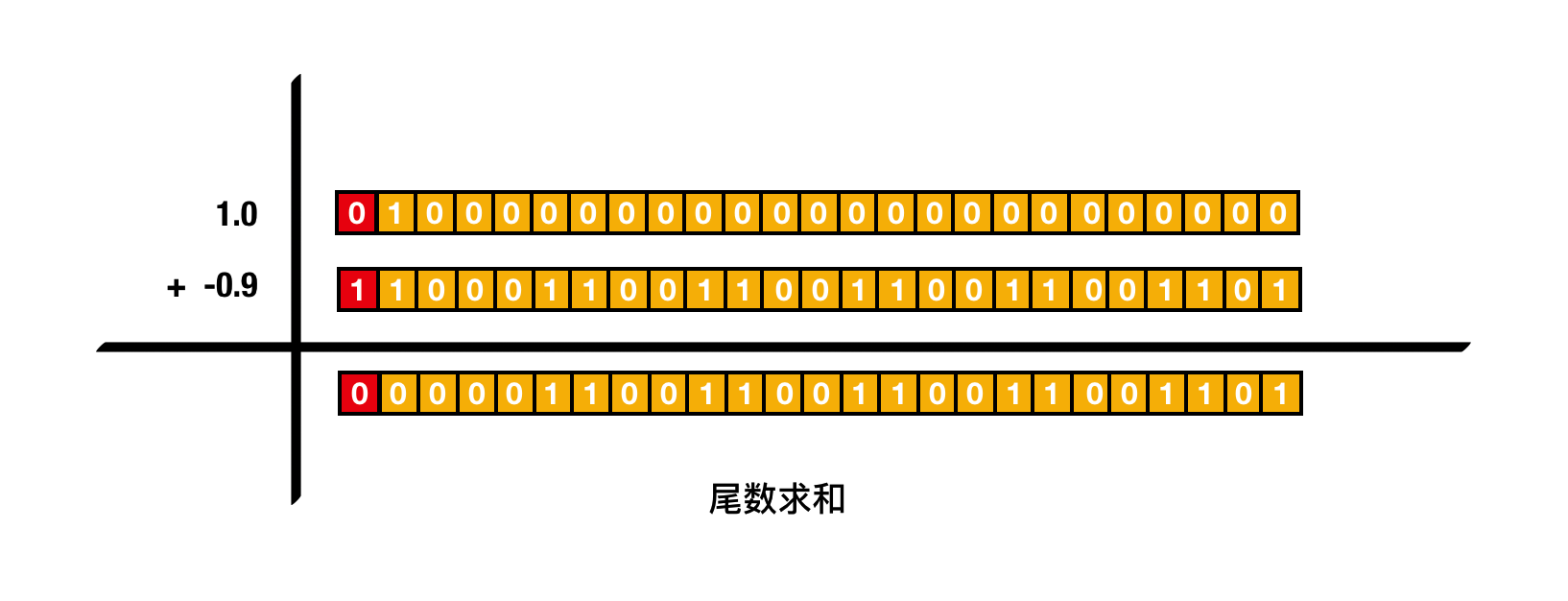
得到尾数位的运算结果为:
0000 - 1100 - 1100 - 1100 - 1100 -1101
结果规格化
尾数求和后的操作并不合乎要求(尾数的最高位必须为1,不明白为什么的同样好好反省下),所以这里我们需要将结果左移4位,同时阶码减4来进行结果规格化。
这样一顿操作后,阶码等于123(对应的二进制为 1111011),尾数为
1100 - 1100 - 1100 - 1100 - 1101 - 0000
再隐藏其尾数的最高位,进而变为:
100 - 1100 - 1100 - 1100 - 1101 - 0000
最终结果
最终,1.0 - 0.9的运算结果为:

最后,我们就得到了一个符号位为0、阶码为01111011、尾数位为100 - 1100 - 1100 - 1100 - 1101 - 0000,对应的十进制表示为0.100000024。
精度损失带来的不良后果
既然浮点数使用时会产生精度损失的问题,那么会给我们的日常开发造成什么影响呢?
使用浮点数大小判断控制某些业务流程时往往产生不可预期的行为。
想象一下这样的场景,电商App,提交订单时需要前端校验用户余额是否足够支付订单,如果不够,就禁用提交订单按钮。
如果不了解精度损失,我们很容易写下这样的判断:
btSubmit.setEnabled(balance >= orderAmount)
如果此时余额或者订单金额丢失了精度,就可能会出现用户余额明明足够支付订单却因为前端错误的判断禁用了提交订单的按钮导致用户无法提交订单(别问我怎么知道这么详细的场景,再问自杀)。

如何避免精度损失带来的不良后果?

避免不必要的使用浮点数.
使用浮点数会带来以下麻烦:性能损耗和精度损失。一般来讲,在 Android 设备上,浮点数要比整数慢约 2 倍。所以,如果某个参数不是无法避免的要使用浮点数类型,更推荐使用整型来替代浮点数类型。
避免不了浮点数使用时,使用双精度浮点数
double来代替float.
首先,在速度方面,float和double在现在的硬件上没有任何区别,在时间和空间的决策上,我相信大部分人都更倾向于使用空间换取时间。同时,得益于更大的存储空间,双精度浮点型的精度比单精度浮点型要高不少。
比如上一部分举到的例子,我们完全可以使用人民中的分作为单位,将余额与订单金额转化成以分作单位的整型比较从而避免因精度损失造成的不可预知的不良后果。
总结
综上所述,计算机中浮点数的精度损失我们避免不了,但是我们可以合理规避掉由于精度损失所造成的不良后果,比如:控制业务流程时避免使用两个浮点数的大小作为判断依据。