先看最终效果:

先说明一下,此效果启发于第二本参考书。
中心红色球是太阳,水蓝色小球是地球。可以看出地球的运行轨道是椭圆,验证了开普勒三定律的第一条。在近日点运行速度比较快,远日点比较慢,符合常识。
你猜测我写这个效果用了多长时间?
不到半个小时吧,其实掌握原理后实现起来还是比较快的。
原理相对来说还是简单的,前提是要使用向量工具。
1. 用向量来思考问题
本系列的前几篇文章,都是使用 x、y 轴分量来计算小球的物理矢量。
fx = f * Math.cos(angle)
fy = f * Math.sin(angle)
ax = fx / ball.m
ay = fy / ball.m
vx += ax
vy += ay
ball.x += vx
ball.y += vy
上述代码中,f 是力,m 是质量,a 是加速度,v 是速度。而带后缀的是相应矢量的分量,比如 fx 是力矢量 f 的横轴分量。
上述运算,本质上还是使用小学的加减法,没有真正用到矢量或者说向量。
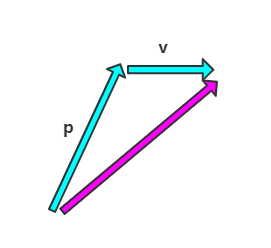
假设我们向量 p 表示小球当前位置,向量 v 表示当前速度,那么下一帧的小球的位置为下图中的粉色向量。不用再分别计算 x 轴 和 y 轴的分量。
为了表示向量这一数据类型,我们简单地封装一个 Vector 类:
class Vector {
constructor(x, y) {
this.x = x
this.y = y
}
scale(n) {
this.x *= n
this.y *= n
return this
}
mag() {
return Math.sqrt(this.x * this.x + this.y * this.y);
}
normalize() {
var m = this.mag()
if (m != 0 && m != 1) {
this.scale(1 / m)
}
return this
}
add(other) {
this.x += other.x
this.y += other.y
return this
}
sub(other) {
this.x -= other.x
this.y -= other.y
return this
}
static add(one, other) {
return new Vector(one.x + other.x, one.y + other.y)
}
static sub(one, other) {
return new Vector(one.x - other.x, one.y - other.y)
}
static dist(one, other) {
var dx = one.x - other.x
var dy = one.y - other.y
return Math.sqrt(dx * dx + dy * dy)
}
}
这些向量操作都很简单,比如 add 表示当前向量加上一个新向量,mag 用来求取向量大小,scale 用来放缩向量的大小,normalize 用于计算单位向量等等。虽然底层仍是 x、y 分量用于计算。但是我们思维的最小单位是向量,层级高了一层。
比如之前的代码用向量的形式表示:
a = f.scale(1 / ball.m)
v.add(a)
ball.p.add(v)
有了向量工具,处理万有引力公式起来就很 easy 了。
2. 动画原理
接下来大体看下开篇动画的原理,看看是否真的简单。
地球人都知道牛顿的万有引力定律这一伟大发现:
任意两个质点有通过连心线方向上的力相互吸引。该引力大小与它们质量的乘积成正比与它们距离的平方成反比,与两物体的化学组成和其间介质种类无关。

其中 G 是万有引力常数,动画里我们简化为 1 就行。
把公式写成代码:
var dist = Vector.dist(sun.p, earth.p)
var f = sun.m * earth.m / (dist * dist)
而这个 f 目前仍是标量,只有大小,没有方向。地球受到的万有引力,方向应该是朝向太阳的,因此完整代码是:
function gravity (sun, earth) {
var dist = Vector.dist(sun.p, earth.p)
var f = sun.m * earth.m / (dist * dist)
var vec = Vector.sub(sun.p, earth.p)
return vec.normalize().scale(f)
}
之所以封装成函数是因为地日之间的万有引力是时刻发生变化的。其中向量 vec 方向是朝向太阳的,对其取单位向量,并放缩大小为 f。这样,最终返回的结果是引力向量。
因此地球的运动核心代码很容易写出来:
var g = gravity(sun, earth)
var a = g.scale(1 / earth.m)
v.add(a)
earth.p.add(v)
核心原理就是这些,剩下就是实现了。
3. 实现
太阳和地球采用的都是小球模型:
class Ball{
constructor() {
this.p = new Vector(0, 0)
this.m = 0
this.radius = 20
this.color = 'white'
}
draw(context) {
context.save()
context.translate(this.p.x, this.p.y)
context.beginPath()
context.arc(0, 0, this.radius, 0, 2 * Math.PI)
context.fillStyle = this.color
context.fill()
context.restore()
}
}
这段代码不是本系列第一次出现了,唯一不同的是原先的 this.x 和 this.y 改用向量 this.p 替换了。
初始化太阳和地球:
var sun = new Ball()
sun.radius = 30
sun.color = 'red'
sun.p = new Vector(canvas.width / 2, canvas.height / 2)
sun.m = 1000
var earth = new Ball()
earth.radius = 3
earth.color = 'aqua'
earth.p = new Vector(canvas.width / 2 + 100, canvas.height / 2 + 80)
earth.m = 1
其中太阳和地球的质量比是 1000: 1。地球的位置比较随便选取了一个位置。
接下来就是原理的核心代码,其中我们假设太阳不动的。
;(function drawFrame() {
window.requestAnimationFrame(drawFrame)
context.clearRect(0, 0, canvas.width, canvas.height)
var g = gravity(sun, earth)
var a = g.scale(1 / earth.m)
v.add(a)
earth.p.add(v)
earth.draw(context)
sun.draw(context)
})()
这里有一个至关重要的点,是地球需要有个初始速度 v 。
不同大小和方向的速度,地球的运行轨道会有所不同。 假如初始速度为 0 向量的话,根据万有引力,地球将会撞向太阳:
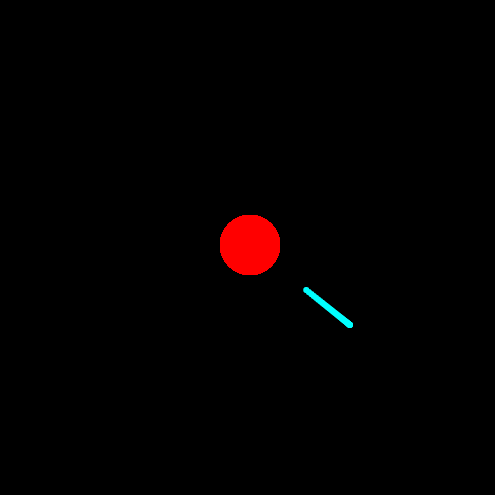
当然这里地球撞上太阳后,没有销毁,但是地球迅速远离太阳。因为速度比较快,万有引力再也拉不回来了。这其实就是三体小说中的“引力弹弓”。
我们让太阳尺寸小点,速度选择为:
var v = new Vector(-0.3, 1)
引力弹弓效果将更好些:

假如速度选择为:
var v = new Vector(-0.8, 1).scale(2.2)
小球将会走圆形轨道:
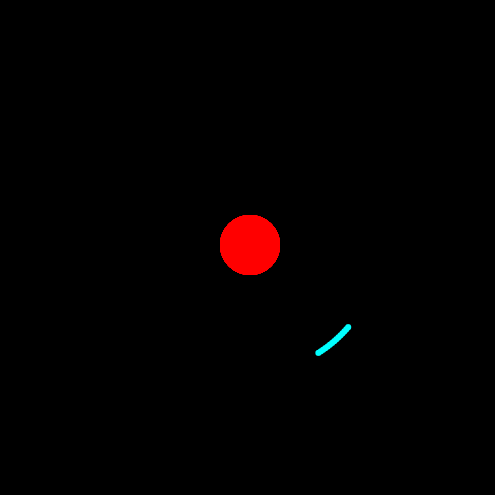
你可以随便调节参数,尝试其他情形,看看效果。
感谢你看到这里,希望有所帮助。
本文完。
下面的内容是关于本系列的介绍。
2019年末,本人立了个flag,2020年要研究透canvas动画技术。

(图中二维码是我的唯一微信号,如有掘友想加的,麻烦备注下【掘金】哈。)
在这个系列,我想写一些常见动画知识,本文是第 5 篇,篇幅可能会长短不一。更多的请查看我的个人主页,或者《系列目录》。
因为篇幅问题,根据以往的经验,赞数不会太多,毕竟大家都喜欢给那种短时间看不完的文章点赞。嗯,我好像也是这样。^_^
其实写文章,主要还是给自己看的,算是自我进步的一个见证吧。抱着这种心态也许能好些。
另外关于canvas技术,我目前完整看完了3本书。算是过了基础一关。
本系列一些文章可能会参考里面的知识体系,对于一些属于领域共识知识,如有局部雷同,只能说:“自己凭本事学来的,怎能算抄袭。。。”。
开玩笑了,想法来源能提一句还是要提一句的。特别喜欢《精英日课》文章里的一段话:

至于文章内容,canvas的API,本系列可能不会准备逐条介绍了,还请初学的童鞋见谅哈。MDN都有的,挺详细的。同时,文章中遇到的还是会简单提下。主要核心是阐述一些技巧和原理层面的知识个人理解吧。另外也打算分析一些codepen上炫酷动画的实现原理,如果有时间可能会分析几个动画引擎,当然都是2D的。
再次感谢你阅读到这里。下一篇文章见。