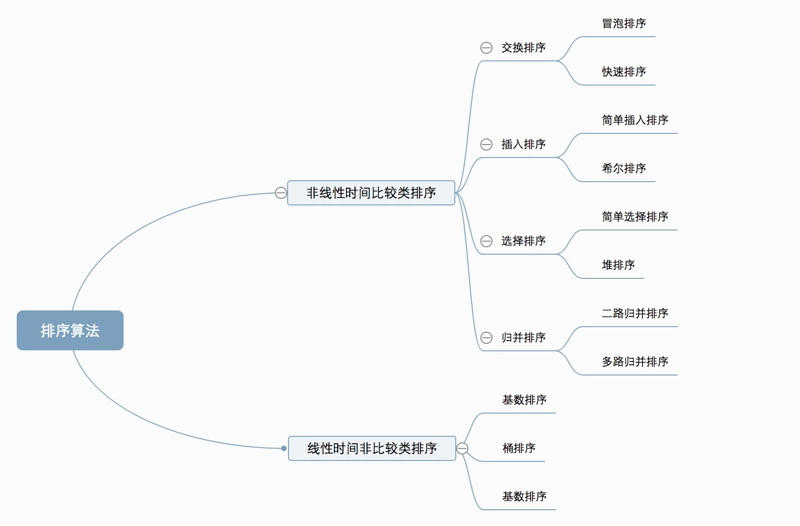
算法分类
十种常见排序算法可以分为两大类:
非线性时间比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此称为非线性时间比较类排序。
线性时间非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。
算法复杂度
相关概念
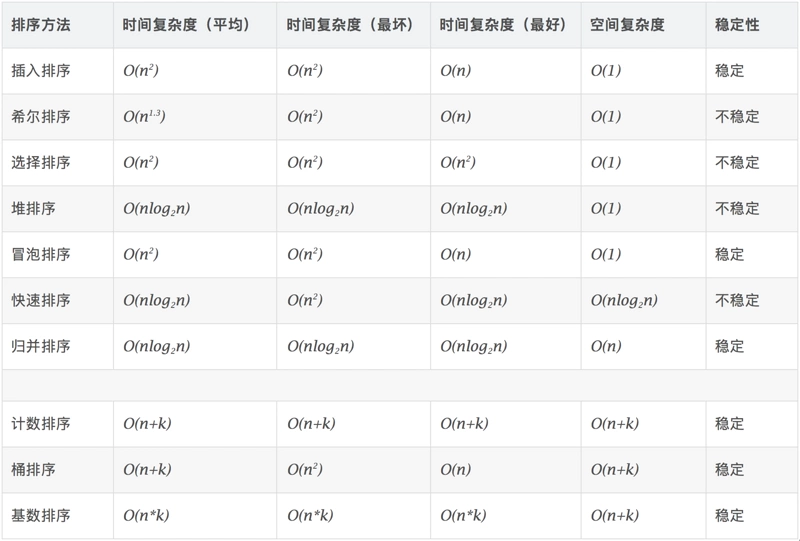
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
冒泡排序(Bubble Sort)
原理:
比较两个相邻的元素,将值大的元素交换到右边
算法描述
- 比较第一位与第二位,如果第一位比第二位大,则交换位置
- 继续比较后面的数,按照同样的方法进行比较,到最后一位的时候,最大的数将被排在最后一位
- 重复进行比较,直到排序完成,注意由于上一次排序使得最后一位已经是最大的数,所以每次排序结束之后,下一次比较的时候可以相应的减少比较数量
动图演示
代码解析
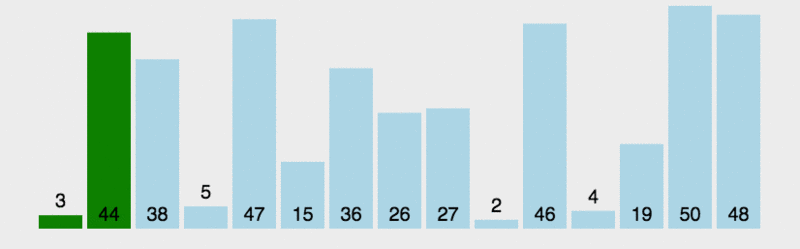
let arr = [3, 45, 16, 8, 65, 15, 36, 22, 19, 1, 96, 12, 56, 12, 45];
let flag;
let len = arr.length;
let num1 = 0; // 比较的次数
let num2 = 0; // 交换的次数
// 有15个数,只需要选出14个最大的数,最后一个数就是最小的,不用进行比较
for(let i = 0; i < len -1 ; i++){
// 每次i变化之后最大的值已经排序到最后一位,无需对最后一位进行比较,所以j的最大值为len-i-1
for(let j = 0; j < len - i - 1; j++){
num1 += 1;
// 如果当前位置的数比下一位置的数大,则交换位置
if(arr[j] > arr[j+1]){
num2 =+ 1;
flag = arr[j];
arr[j] = arr[j+1];
arr[j+1] = flag
}
}
}
console.log(arr,num);
输出的结果为:

计数器num1和num2的值分别为:105和46
从代码中看出,排序过程中,所需要的临时变量一直都没有变化,因此空间复杂度为O(1);代码进行了两次for循环且是嵌套循环,因此时间复杂度为O(n²)。
冒泡排序的最优情况是原数组默认正序排序,此时比较的次数num1仍为105,而交换次数num2为0,此时的时间复杂度仍然为O(n²),那么为什么前面的复杂度表格中说是O(n)呢?经过一番研究发现,需要对上述代码进行简单优化。

如果排序的数组是:[1,2,3,4,5],此时完全符合最优复杂度情况,当我们进行第一次循环发现,两两相邻的数据一次都没有进行交换,也就是说所有的数都比前一个数大,此时就是正序,无需再进行下次排序,所以我们只需要加上一个变量进行判断:
// 初始未产生交换
let isSwap = false;
for(let i = 0; i < len -1 ; i++){
// 每次i变化之后最大的值已经排序到最后一位,无需对最后一位进行比较,所以j的最大值为len-i-1
for(let j = 0; j < len - i - 1; j++){
num1 += 1;
// 如果当前位置的数比下一位置的数大,则交换位置
if(arr[j] > arr[j+1]){
num2 =+ 1;
isSwap = true;
flag = arr[j];
arr[j] = arr[j+1];
arr[j+1] = flag
}
}
// 如果产生交换,直接结束循环
if(!isSwap){
return
}
}
当产生交换时,isSwap变成true,第一次循环结束之后,如果isSwap如果还是false表示未经过交换,数组已经是正序,无需继续排序,此时的时间复杂度为O(n)
在比较过程中只判断了大于后一个数,如果两个数相等无需交换,所以冒泡排序是稳定的排序。
选择排序(Selection Sort)
原理
将序列分为未排序和已排序,从未排序序列中找到最小的数,放到无序序列起始位置,然后继续从剩余未排序序列中继续寻找最小值
算法描述
- 初始无序序列为待排序序列,有序序列为空
- 从无序序列中找到最小值,放到无序序列起始位置,也就是和起始位置交换
- 将无序序列起始位向后推一个位置,继续2步骤
动图演示
代码解析
// 选择出无序序列中最小的值放到无序第一位
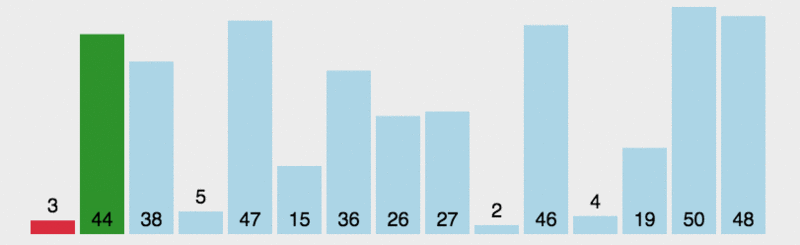
let arr = [3, 45, 16, 8, 65, 15, 36, 22, 19, 1, 96, 12, 56, 12, 45];
let len = arr.length;
let minIndex;
let flag;
let num1 = 0; // 比较次数
let num2 = 0; // 交换次数
for(let i = 0; i < len - 1;i++){
// 每次选择最小值之后,无序区的开始位置往后推1
minIndex = i;
// j循环到最后一位,选择出当前无序数组中数值最小的索引值
for(let j = i + 1; j < len;j++){
num1 += 1;
if(arr[minIndex]>arr[j]){
minIndex = j;
}
}
num2 += 1;
flag = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = flag;
}
console.log(arr,num1,num2)
输出结果为:

计数器num1和num2的值分别为:105和14
也就是说,选择排序的比较次数和冒泡排序未优化时一样,而交换的次数只有14次
再举刚刚的栗子:[1,2,3,4,5],正序序列,无需进行任何交换,我们对最后交换代码进行优化:
if(minIndex == i){
num2 += 1;
flag = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = flag;
}
此时没有发生数据交换。
其实从代码中可以看到,无论如何,选择排序总会经过N^2/2次比较,而受原始数列影响,交换的次数最大为n-1,最小次数为0。
因此选择排序时间复杂度总为:O(n平方),空间复杂度为:O(1)
选择排序是不稳定的,为什么这么说,看个栗子:[5,3,8,5,2],好了不说也能看出来了。
插入排序(Insertion Sort)
原理
构建有序序列,对于未排序的数据,从有序序列后向前扫描,找到相应位置插入
动图演示
代码实现
let arr = [3, 45, 16, 8, 65, 15, 36, 22, 19, 1, 96, 12, 56, 12, 45];
let len = arr.length;
// 定义当前未排序数据起始位置值也就是即将插入的数据
let currentValue;
// 有序序列遍历位置
let preIndex;
let num1 = 0; // 比较次数
let num2 = 0; // 交换次数
for(let i = 1;i < len; i++){
// 定义原始数据第二位为未排序数据第一位,默认原始数据第一位已排序
currentValue = arr[i];
// 当前有序序列最大索引
preIndex = i - 1;
// 当索引大于等于0且当前索引值大于需要插入的数据时
for(let j = preIndex;j>=0;j--){
// 第一次比较,如果有序序列最大索引值其实就是待插入数据前一位,比待插入数据大,则后移一位
num1+=1;
if(arr[preIndex]>currentValue){
arr[preIndex+1] = arr[preIndex];
preIndex --;
// 索引减1,继续向前比较
}
}
// 当出现索引所在位置值比待插入数据小时,将待插入数据插入
// 为什么是preIndex+1,因为在while循环里面后移一位之后,当前索引已经变化
num2 += 1;
arr[preIndex+1] = currentValue;
}
console.log(...arr,num1,num2)
输出的结果为:

计数器num1和num2的值分别为:105和14
插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
在时间复杂度上,如果按照上述写法,执行的次数依次为,1,2,3....n-1,因此时间复杂度为O(n²)

冒泡排序出现了优化之后最优复杂度变小的情况,看看前面的表格,插入排序的最优时间复杂度为O(n),那么这又是什么原因呢?
我们看看判断待插入值是否小于当前索引位置值的地方,用了一个for循环和一个if,我们能不能改写一下呢?
while(preIndex>=0&&arr[preIndex]>currentValue){
arr[preIndex+1] = arr[preIndex];
preIndex --;
}
这样看,如果在正序情况下:[1,2,3,4,5],每次比较都不会进入while循环,因此只执行了n-1次比较操作,因此此时时间复杂度为O(n),那么最坏复杂度其实也就是逆序情况了,需要执行1,2,3...n次,因此最坏时间复杂度为O(n²)。
总结
综合比较一下最简单的三种排序方法:
选择排序在冒泡排序上做了优化,冒泡排序两两比较每一轮选出一个最大值,而选择排序则从序列中直接选择出最小值插入无序序列首部(进行交换),相对于冒泡排序减少了不必要的换位操作。
插入排序在思想上和选择排序差不多,选择排序是从无序序列中找出最小值,与无序序列的首位进行交换,从而生成一个有序序列,而插入排序则从无序序列中直接选出首位,将首位与有序序列进行比较,插入相应的位置。
使用场景
对于一般工作来说,这三种使用没什么体验上的差距
如果非要选择的话,插入排序比选择排序少一些比较的次数,但选择排序有时候比插入排序少挪动次数,建议数据较大时用插入排序,数据量较小时可以用选择排序。(其实这俩差不多--)
参考
新手上路请多指教,如有错误,轻喷