深度学习与物理，有效场论，重整化群，简介1608.08225

2018-12-03 648 阅读7分钟

原文链接： zhuanlan.zhihu.com

之前提到2017年的一篇文章《Why does deep and cheap learning work so well》（https://arxiv.org/pdf/1608.08225.pdf），知乎还没有朋友写过，这里简单介绍。其中作者希望从物理的角度解释深度学习的有效性。

1. 从物理/统计模型看机器学习

首先从物理/统计模型的角度，考虑常见的机器学习问题：

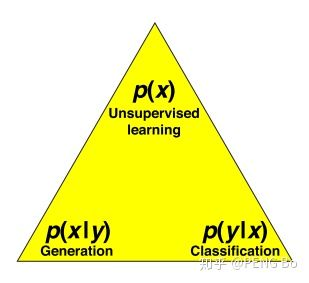
令 x 为数据，令 y 为生成 x 的物理模型的输入。
例如 y 可能是 {猫, 狗, 人, 牛, 马 …}，x 是对应的各种图像。
生成问题是找到 p(x|y)，即从类别 y 到图像 x。
分类问题是找到 p(y|x)，即从图像 x 到类别 y。

2. 深度学习的参数真的很多吗？

文中把深度学习叫 Cheap Learning，其实意思不是说学习方法简单（SGD），而是说深度学习的参数并不多（比起它希望描述的事物）：

一张 100 万像素的 8-bit 彩色图片，有256^3000000 种可能性。
如果自然图片及其分类是完全随机的，解决图像问题就需要海量的神经元。
只有极少的图片属于日常生活中可能拍摄到的图片。所以，深度神经网络才得以用较少参数（例如几千万个）解决图像问题。几千万个参数并不多！
后文会进一步解释，为什么深度网络用较少的参数就可以拟合自然图片。

3. 深度学习，是在学 Hamiltonian

具体以图像分类为例。不妨认为图像的生成模型 p(x|y) 是一个 Boltzmann 分布：

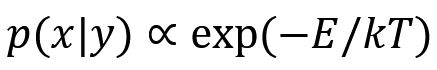
忽略因子，我们下面直接这样定义 Hamiltonian：

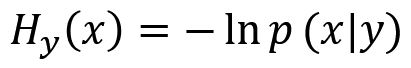
图像分类问题是求 p(y|x)，根据 Bayes 公式：

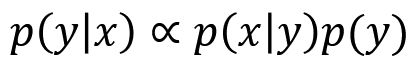
那么我们再定义 $\mu_y = -\ln p(y)$ ，则：

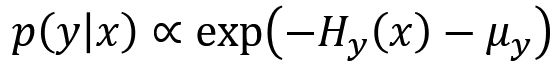
现在我们宣称，如果我们的图像分类网络的最后一层是 SoftMax 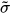$\tilde\sigma$ ：

那么倒数第二层就是在拟合 Hamiltonian。因为，此时也可以将网络的输出写成这样：

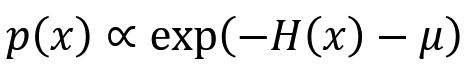
其中 H 是倒数第二层的输出（在加偏置之前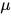）， $\mu$ 是倒数第二层的偏置。可以看到恰好是一样的形式。

4. 深度网络，适合学习物理中的 Hamiltonian

物理中的 Hamiltonian，可以写成级数展开：

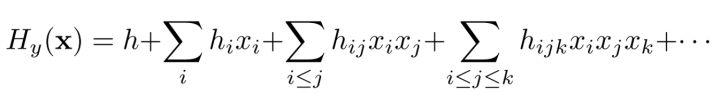
而且，这里的低阶项往往更重要，所以神经网络用较少的参数就可以拟合 Hamiltonian。

为什么低阶项往往更重要？可以用重整化群的观点解释，稍后就会说。

深度网络适合学习这种 Hamiltonian。具体演算可参见论文。简单地说，神经网络主要是乘法和加法，所以适合学习多项式形式的级数展开。网络的非线性也可以展开成为级数嘛。

最近也有研究者认为直接用多项式学习的效果就不错：

https://arxiv.org/pdf/1806.06850.pdfarxiv.org

5. 有效场论：信息的提纯

看图：

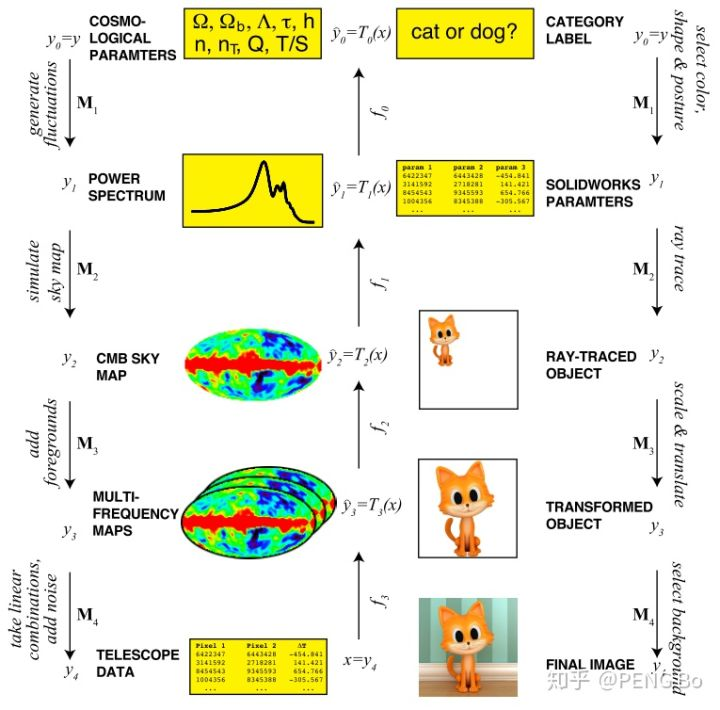
从 y 到 x，就像从 {猫} 到猫的具体图片，就像从宇宙的基本常数到具体观测到的宇宙，这个过程有很多我们不关心的噪音参数。

在机器学习问题中，我们通常只关心宏观的参数，例如图片是猫还是狗，而不关心“每一根毛是什么朝向”“(123,456)坐标的点是什么颜色”等等微观的噪音参数。

这就像做物理时，很多时候更关心物体的宏观行为，那么用质量，温度等等少数宏观参数就可以概括物体的宏观行为。虽然物体中实际有极其大量的微观粒子和极其复杂的微观运动模式，但这些细节噪音对于宏观行为并不重要。

这就是有效场论，从大量参数中，提炼出与宏观行为有关的参数。这些宏观参数往往就来自于 Hamiltonian 的低阶项。为什么？可以用重整化群的观点解释。

6. 重整化的起源：来自于量子场论

我们先简单谈谈重整化（renormalization），它起源于量子场论。例如，在 QED 中，用费曼图做微扰展开，带圈的图容易导致发散，因为在路径积分中，需考虑圈中的虚粒子有任意动量/能量的情况，例如下面右边的这个图对应的积分算出来是发散的。

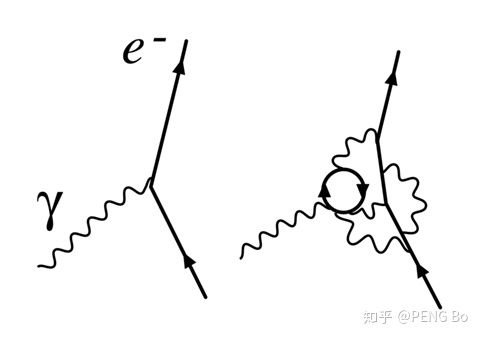
但是，可以手动设置一个积分的能量截止点，然后要求公式中的耦合常数、电子质量等等与此能量有关，最终可以实现：积分与能量截止点无关（这是必须的，因为能量截止点是非物理的），而且发散被“吸收”了，积分可以算出来结果了。

这叫做 running couplings，耦合常数不是固定的，而是与能标有关。实验也证实了这一点。

下面是经典的图，电磁力随着能标上升越来越强，强力随着能标上升越来越弱，在加入超对称后有“大统一”的可能性。

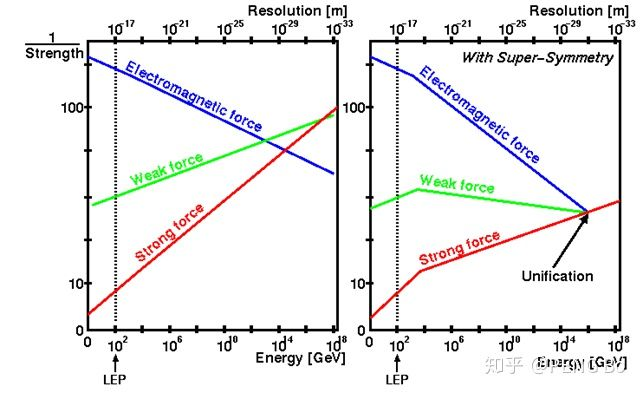
7. 从重整化到重整化群：在凝聚态问题的发展

量子场论的重整化，是希望路径积分的结果具有“标度不变”（scale invariant）。

在凝聚态问题中，我们也很关心系统何时处于“标度不变”（自相似 / 分形 / 临界）状态，因此发展出了重整化群概念。

例如，这是著名的 Ising 模型，在不同温度的典型情况：

左边，是温度很低，很固定，很无聊。

右边，是温度很高，很混乱，很无聊。

有趣的是中间的相变温度 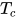T_c ，此时系统在秩序与混沌之间的临界状态，自相似的状态。

怎么把相变温度 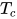T_c 计算出来？有趣的思路是：因为此时系统是自相似，所以我们在不同尺度看，它应该拥有一样的统计规律。

如下图所示，如果我们只看白格点（这叫做粗粒化），应拥有与全体点相同的统计规律。

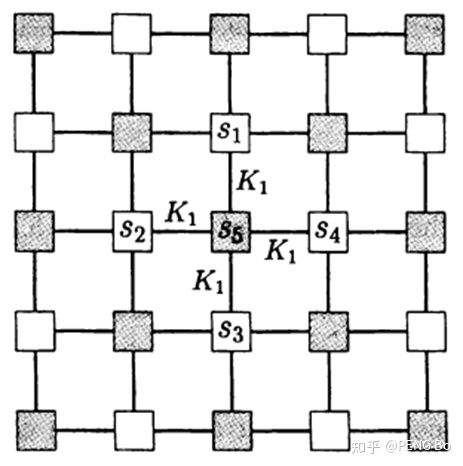
要求粗粒化后的统计规律一致（具体有些细节，需要引入新系数），就可以得到重整化方程（粗粒化操作就是重整化操作的一种），就可以解出临界温度。

重整化操作，构成重整化群，作用在系统的参数向量上，不断作用就形成重整化流，不动点就对应临界参数。

8. 临界现象：自相似，长程相关，幂律

系统在临界状态时，还有一些值得一提的特点。以 Ising 模型为例，我们定义关联：

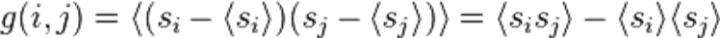
当温度 T 远离相变温度 Tc，关联随距离 r 衰减很快：

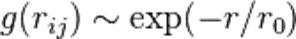
但 T ~ Tc 时，关联为幂率（power law）衰减：

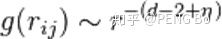
如果还用指数衰减描述去拟合，会发现 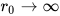$r_0 \rightarrow \infty$ ，这就叫做长程相关。

自然图像是符合长程相关的。鸟群、昆虫群、细菌簇、人脑等等，都处于临界状态：一个小小的信号有可能引起雪崩效应，这样才能实现信息的快速传递。

9. 复杂系统的宏观特征

回到之前的问题：为什么 Hamiltonian 的低阶项对于宏观行为更重要。不妨看个简单模型，令图像为一个连续的场 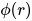$\phi(r)$ ，定义 quadratic Hamiltonian：

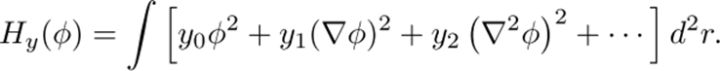
如果将图像粗粒化 b 倍，要求 H 不变，则：

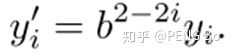
可见，如果不断粗粒化，只有低阶项 y0 y1 是值得考虑的参数。这少数参数，对应机器学习中的“特征”，其余参数对应“噪音”。

做物理的有效场论，与做机器学习类似，都是找到并拟合“特征”。

10. 深度网络的有效性

文中最后还计算了一些话题。例如，虽然根据通用逼近定理，用浅层网络可以拟合一切问题，但是，对于一些用深度网络+较少的神经元可以解决的问题，用浅层网络去拟合就可能会需要多得多的神经元。

另外，前文说过，网络是在拟合 Hamiltonian，如果 Hamiltonian 具有层级性，那么深度网络的层级性就更符合 Hamiltonian 的过程。例如，如果生成模型是一层层的马尔可夫链：

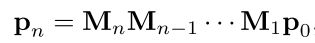
这就和深度网络的不断矩阵乘法可以对应。

友情链接：